【中2数学】三角形の合同の証明のポイント・練習問題

中２数学の「証明」について、しくみ・流れから代表問題の解法パターンまでふれています。それでは、中２数学の「証明」をみていきましょう。

証明とは？

証明とは、あることことがらが成り立つことを、すじ道を建てて明らかにすることです。

「ＡならばＢである」のような形でいい表されることがらの、Ａの部分を「仮定」（与えられてあらかじめわかっていること）、Ｂの部分を「結論」（Ａから導こうとしていること）といいます。

●例題
次のことがらについて、仮定と結論をそれぞれ答えよ。

（1）2つの直線が平行ならば、同位角は等しい。
（2）ｘが15の倍数ならば、ｘは3の倍数である。

●解説
「ＡならばＢである」のような形でいい表されることがらで、Ａの部分を「仮定」、Ｂの部分を「結論」というので、

●解答
（1）仮定…2つの直線が平行　結論…同位角は等しい
（2）仮定…ｘが15の倍数　結論…ｘは3の倍数

＜合同な三角形を証明する場合＞

△（　　　　）と△（　　　　　）において
（　　　）＝（　　　）（根拠・理由）…①
（　　　）＝（　　　）（根拠・理由）…②
（　　　）＝（　　　）（根拠・理由）…③
①②③より（　合同条件　）より
△（　　　　）≡△（　　　　　）

●三角形の合同条件
➊3辺がそれぞれ等しい
➋2辺とその間の角がそれぞれ等しい
➌1辺とその両端の角がそれぞれ等しい

●直角三角形の合同条件
➊斜辺と他の1辺がそれぞれ等しい
➋斜辺と1つの鋭角がそれぞれ等しい

など

次の図の2つの直角三角形が合同になることを「直角三角形の斜辺と1つの鋭角がそれぞれ等しいとき、三角形は合同になること」を証明します。

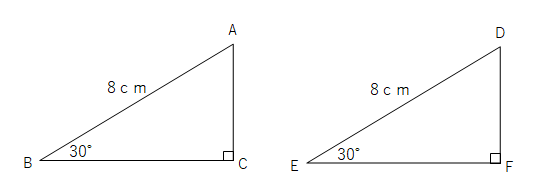
△ABCと△DEFにおいて
仮定より　AB＝DE…①
仮定より　∠ABC＝∠DEF=30°…②
三角形の内角の和は180°だから　∠BAC=∠EDF…③
①②③より　1組の辺とその両端の角がそれぞれ等しいので、
△ABC≡△DEF

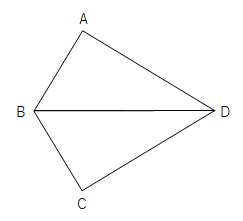
【問1】次の図で、ＡＢ＝ＣＢ、ＢＤは∠ＡＢＣの二等分線です。このとき。ＡＤ＝ＣＤとなることを証明せよ。

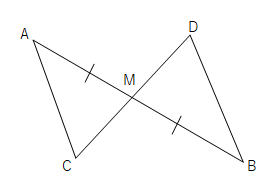
【問2】次の図で、線分ＡＢの中点をＭとし、Ｍを通る線分ＣＤを∠ＣＡＭ＝∠ＤＢＭとなるようにとると、ＡＣ＝ＢＤになることを証明せよ。

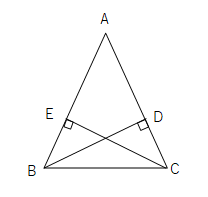
【問3】次の図で、AB＝ACの二等辺三角形ABCで、頂点Bから辺ACに垂線をひき、その交点をD、また、頂点Cから辺ABに垂線をひき、その交点をEとします。このときAD＝AEになることを証明せよ。

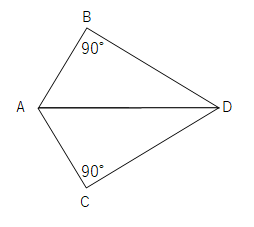
【問4】次の図のように、BD＝CDが等しく、∠ABD＝∠ACD＝90°の2つの三角形があるとき、∠ADB＝∠ADCであることを証明せよ。

【問1】
△ＡＢＤと△ＣＢＤにおいて
仮定より　ＡＢ＝ＣＢ…①
仮定より　∠ＡＢＤ＝∠ＣＢＤ…②
共通な辺より　ＢＤ＝ＢＤ…③　（ＢＤは共通でも）
①②③より、2組の辺とその間の角がそれぞれの等しいので
△ＡＢＤ≡△ＣＢＤ
合同な図形では、対応する辺の長さは等しいので、
ＡＣ＝ＣＤ

【問2】
△ＡＣＭと△ＢＤＭにおいて
仮定より　ＡＭ＝ＢＭ…①
仮定より　∠ＣＡＭ＝∠ＤＢＭ…②
対頂角より　∠ＡＭＣ＝∠ＢＭＤ…③
①②③より、1組の辺とその両端の角がそれぞれ等しいので
△ＡＣＭ≡△ＢＤＭ
合同な図形では、対応する辺の長さは等しいので、ＡＣ＝ＢＤ

【問3】
△ABDと△ACEにおいて
仮定より　AB＝AC…①
∠ADB＝∠AEC＝90°…②
共通な角より　∠BAD＝∠CAE…③
①②③より　直角三角形の斜辺と1つの鋭角がそれぞれ等しいので、
△ABD≡△ACE

直角三角形の合同の証明のポイント
直角三角形の合同条件を使った証明では、次のことを頭においておきましょう。

以上であれば、直角三角形の合同条件を使った証明ができます。

【問4】
△ABDと△ACDにおいて
仮定より　BD＝CD…①
仮定より、∠ABD＝∠ACD＝90°…②
共通な辺より　AD＝AD…③
①②③より、直角三角形の斜辺と他の1辺がそれぞれ等しいので
△ABD≡△ACD
合同な図形では、対応する角は等しいので、
∠ADB＝∠ADC