ばねの計算問題、フックの法則に関する練習問題です。まずは、確認問題で基本用語の確認を行い。次に練習問題で実力を伸ばしましょう。
ばね・フックの法則の確認問題
- ばねのように、元に戻ろうとする性質を何というか。
- ばねのように、元に戻ろうとする力を何というか。
- ばねにはたらく強さとばねののびが比例することを何というか。
- 何もつるしていないときのばねの長さを何というか。
- 1.0Nのおもりをつるすと5.0cm伸びるばねに0.8Nのおもりをつるすと、ばねののびは何cmになるか。
- 何もつるしていないときの長さが10cmのばねに、1.0Nのおもりをつるすと、ばねの長さが12cmになった。このばねに4.0Nのおもりをつるすと、何cmの長さになるか。
解答
- 弾性
- 弾性力
- フックの法則
- 自然長
- 4.0cm
- 18cm
【練習問題❶】ばねの計算問題
下の図のようにばねに50gのおもりを1個つり下げたところばね全体の長さが25cmになった。次に50gのばねを2個つり下げたところ、ばね全体の長さが29cmになった。グラフはこのときのばねにつり下げたおもりの質量とばねののびをまとめたものである。100gの物体にはたらく重量を1Nとして、次の各問いに答えよ。
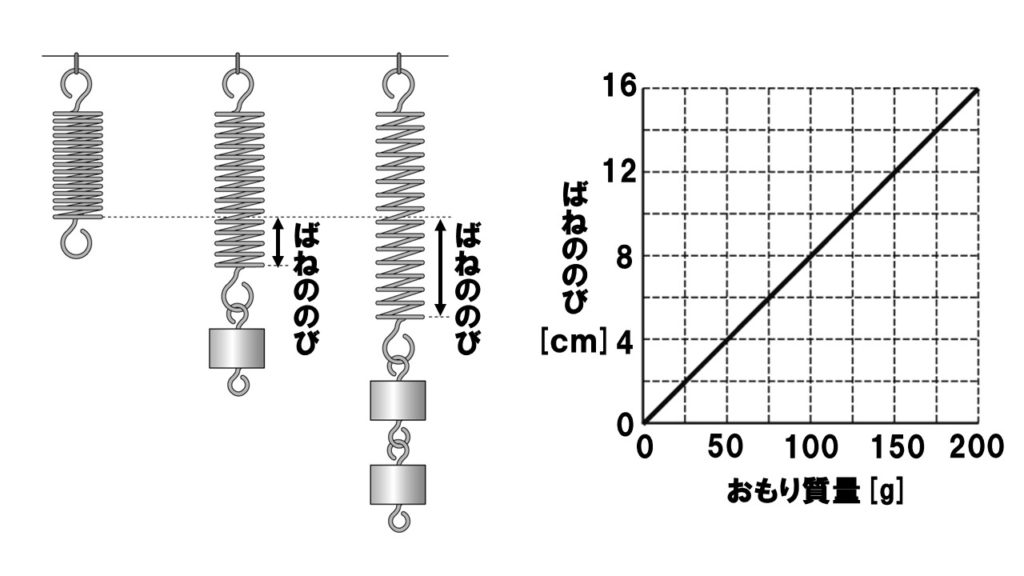
(1)実験の結果から、ばねののびとおもりの質量にはどのような関係があるとわかるか。
(2)このばねは1Nあたり何cm伸びるばねか。
(3)何もつるしていないときのばねの長さは何cmか。
(4)このばねに300gのおもりをつるすと何cmののびになるか。
(5)このばねに150gのおもりをつるすと、ばね全体の長さは何cmになるか。
(6)このばねの長さが41cmになるには、50gのおもりを何個つるせばよいか。
(7)このばねを2本並列につなぎ100gのおもりをつるすと、ばねの長さは何cmになるか。
【解答・解説❶】ばねの計算問題
(1)比例関係
グラフが原点を通る直線なので、ばねののびとおもりの質量には比例関係があるとわかります。
(2)8cm
1Nは100gの重さになるので、グラフより100gのおもりをつるすと8cm伸びるとわかる。
(3)21cm
グラフから50gのおもりをつるすとばねが4cm伸びるとわかります。また、問題文より50gのおもりをつるしているとき、ばね全体の長さが25cmになっているので、何もつるしていないときのばねの長さ(自然長)は、
25cm-4cm=21cm
になります。
(4)24cm
2より1N(100g)のおもりをつるすと8cm伸びるとわかったので、3N(300g)のおもりをつるすと、
1N:8cm=3N:xcm
x=24cm
ばねは24cm伸びるとわかる。
(5)33cm
2より1N(100g)のおもりをつるすと8cm伸びるとわかったので、1.5N(150g)のおもりをつるすと、
1N:8cm=1.5N:xcm
x=12cm (※グラフから12cmを読み取っても良い)
これに、何もつり下げていないときのばねの長さを加えると、
12cm+21cm=33cm
(6)5個
ばねの長さが41cmのとき、ばねののびは、
41cm-21cm=20cm
ばねが20cm伸びるためには、
1N:8cm=xN:20cm
x=2.5N
2.5Nは250gなので、
250g÷50g=5個
50gのおもりを5個つるせばよいとわかる。
(7)25cm
ばねを並列につなぐと、おもりの重さが2つに均等に分かれて加わるので、
1N(100g)÷2本=0.5N(50g)
の重さが並列につないだばね1本あたりに加わることになる。
グラフより0.5N(50g)のおもりをつり下げると4cm伸びることから、ばねの長さは、
4cm+21cm=25cm
となる。
【練習問題❷】ばねを水平に引く問題
ばねAとさまざまな質量のおもりを用いて、次の実験1と実験2を行った。これについて、後の各問いに答えよ。ただし、実験に登場するばねや糸の重さは無視できるものとし、100gの質量にはたらく重量を1.0Nとする。
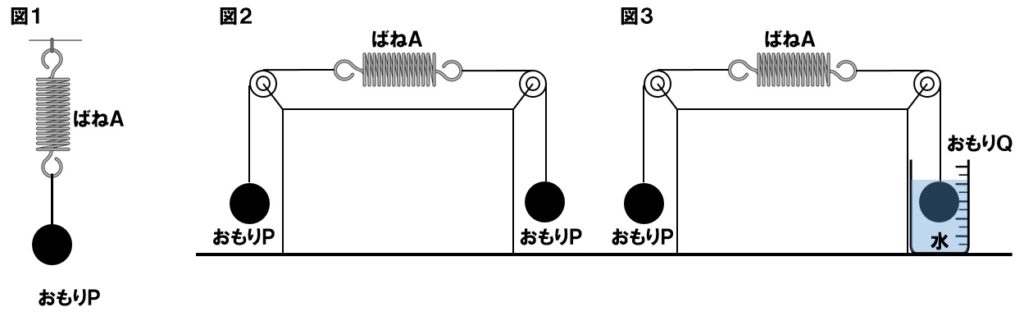
(1)実験1で、ばねAに質量250gのおもりPをつるすと、ばねAの伸びは何cmになるか。
(2)実験2で、ばねの両端に質量250gのおもりPをそれぞれつるすと、ばねAの長さは何cmになるか。
(3)実験3で、おもりQにはたらく浮力は何Nになるか。
(4)実験3で、ばねAの伸びは何cmになるか。
【解答・解説❷】ばねを水平に引く問題
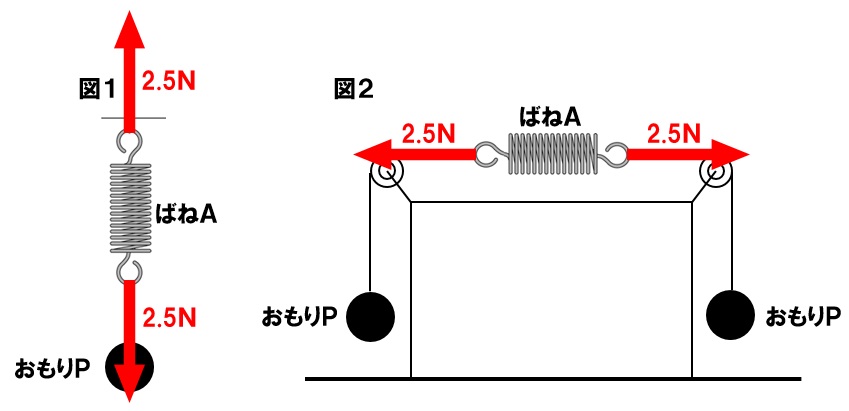
(1)10cm
表より、50gおもりの質量が増加すると、ばねが2cm伸びていることから、ばねに何もつるしていないときの長さ(自然長)は、10cm-2cm=8cmであるとわかります。表から250gの重しをつるすと、ばねの長さが18cmになっていることから、
18cm-8cm=10cm
ばねの伸びは10cmであるとわかります。
(2)18cm
おもりPを、図1と図2のようにつりさげた場合、ばねAに加わる力の大きさは同じになります。図1では、ばねPはおもりによって下向きに2.5N、天井によって上向きに2.5Nで引かれています。図2でも、ばねPはおもりによって右向きに2.5N、左向きに2.5Nで引かれています。つまり、図1も図2も両側から2.5Nずつで引かれていることになります。したがって、ばねののびは10cm、自然長8cmを足して、ばねの長さは18cmになります。
(3)0.7N
ばねAの左側に質量250gのおもりPがつりさげてあり、それとばねの右側に、水の中に入れてつりさげてある質量320gのおもりQがつりあっているので、下の図のようにおもりQには水の中で受ける上向きの力である浮力が生じています。その大きさは、
3.2N-2.5N=0.7N になります。
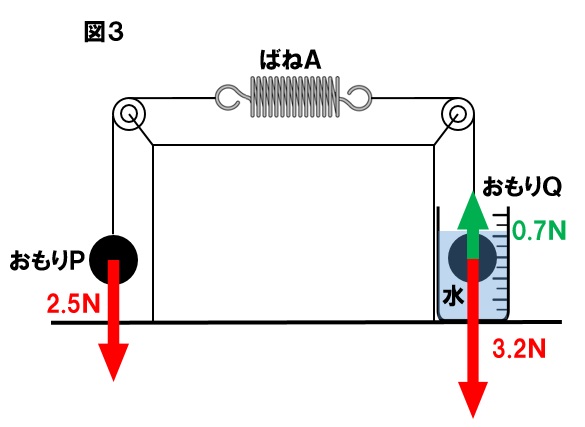
(4)10cm
おもりQには浮力が0.7N生じているので、結局、ばねAは両側から2.5Nで引っ張られていることになります。したがって、実験2の図2と同じ状態になります。ばねののびと、ばねの長さのどちらを問われているのか注意しながら解答するようにしましょう。



コメント