【中1理科】地震波の速さ・地震発生時刻・初期微動継続時間の求め方です。地震の基礎知識を確認しましたが、今回は地震の計算について見ていきます。地震波の速さを計算したり、距離・時間を求めたりします。
地震の計算問題
地震の単元で登場する計算問題は大きく3つのタイプの計算問題に分類さることができます。大森公式などを使った応用的な計算は置いておいて、次の3つの計算方法をマスターしましょう。
- P波やS波の速さの計算
- 地震発生時刻を求める計算
- 初期微動継続時間に関する計算
この3つは基本的な計算をすることで簡単に求めることができます。しっかりと練習して得点につなげてください。
P波やS波の速さの計算
速さの計算をするのですから、「距離」と「時間」をグラフなどから読み取り、距離÷時間の計算をするだけです。
- 地震の波の速さ[km/s]=距離[km]÷時間[秒]
グラフから速さを求める
次の地震のグラフからP波とS波の速さを求めてみましょう。
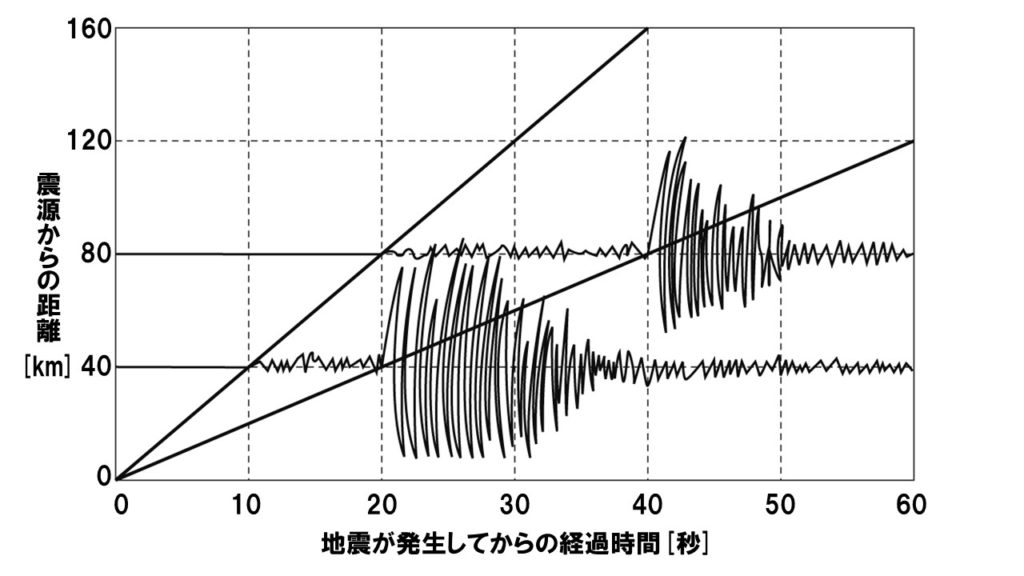
P波とS波の速さを求めるので、グラフから距離と、その距離を進むのにかかった時間を読み取ります。どこでもいいのでP波とS波のグラフの格子点を通っているところを2点探してください。
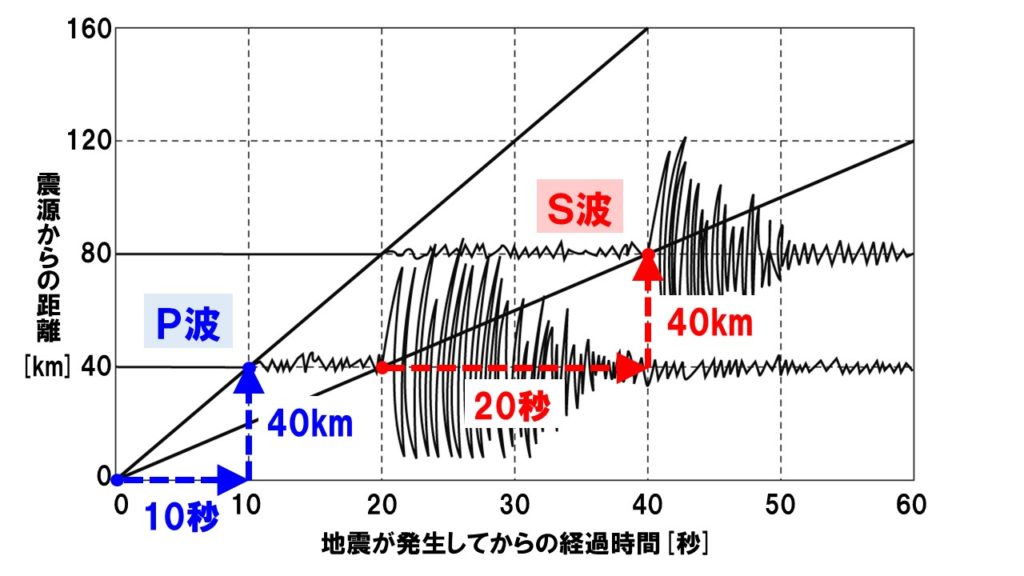
上の図のように、適当にそれぞれ2点を選んでみました。どこでもいいのですが、計算しやすい数字になるところを選んでください。
- P波の速さを求める
グラフから40kmの距離を10秒かかったことがわかります。
40km÷10秒=4km/s - S波の速さを求める
グラフから40kmの距離を20秒かかったことがわかります。
40km÷20秒=2km/s
適当に作ったグラフですので、P波の速さが4km/s、S波の速さが2km/sと極端に遅い結果になりましたが、実際はだいたいP波が8km/s、S波が4km/s程度になります。
表から速さを求める
次は表からP波とS波の速さを求めてみましょう。
| 震源からの距離 | 初期微動が始まった時刻 | 主要動が始まった時刻 |
| 160km | 午前7時24分35秒 | 午前7時24分47秒 |
| 320km | 午前7時24分55秒 | 午前7時25分27秒 |
初期微動が始まった時刻が観測地点にP波が到着した時刻で、主要動が始まった時刻がS波が到着した時刻です。
- P波の速さを求める
表の2地点間の距離は、
320km-160km=160km
P波が160kmの距離を進むのにかかった時間は、
午前7時24分55秒-午前7時24分35秒=20秒
P波の速さは、
160km÷20秒=8km/s - S波の速さを求める
表の2地点間の距離は、
320km-160km=160km
S波が160kmの距離を進むのにかかった時間は、
午前7時25分27秒-午前7時24分47秒=40秒
S波の速さは、
160km÷40秒=4km/s
地震発生時刻を求める
グラフから読み取ることもできますが、計算で求める方法を今回説明します。次の手順で計算していきましょう。
| 震源からの距離 | 初期微動が始まった時刻 | 主要動が始まった時刻 |
| 160km | 午前7時24分35秒 | 午前7時24分47秒 |
| 320km | 午前7時24分55秒 | 午前7時25分27秒 |
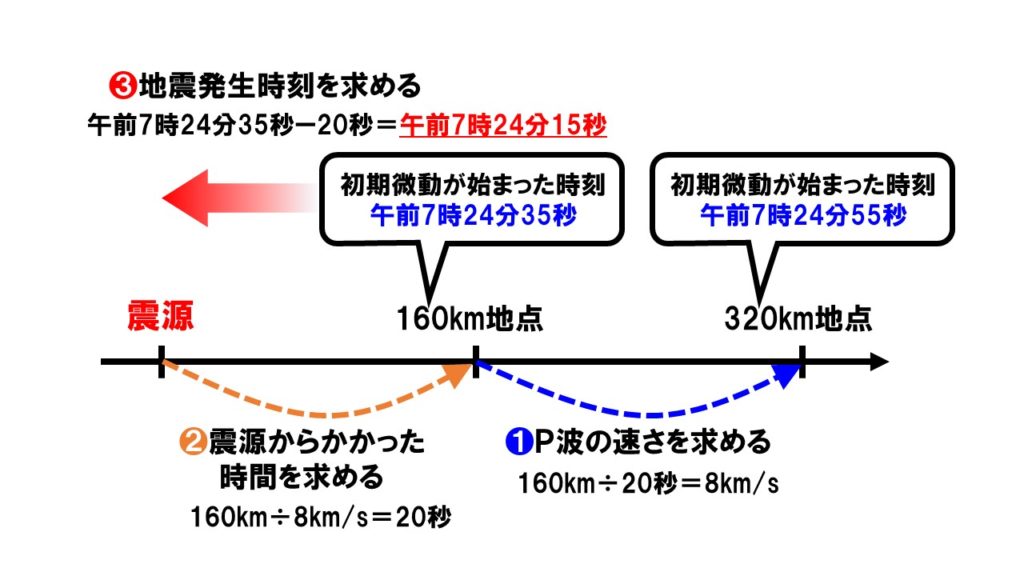
- P波やS波の速さを求める
160km÷20秒=8km/s - 震源からP波やS波が進むのにかかった時間を計算する
160km÷8km/s=20秒 - 地震発生時刻を求める
午前7時24分35秒-20秒=午前7時24分15秒
初期微動継続時間に関する計算
P波が到着してSが到着するまでの初期微動が続く時間を初期微動継続時間といいました。この初期微動継続時間は震源からの距離に比例して長くなります。
この比例関係を使った計算問題が出題されます。
| 震源からの距離 | 初期微動が始まった時刻 | 主要動が始まった時刻 |
| 160km | 午前7時24分35秒 | 午前7時24分47秒 |
| 320km | 午前7時24分55秒 | 午前7時25分19秒 |
上の表で、震源からの距離が160km地点での初期微動継続時間は、
午前7時24分47秒-午前7時24分35秒=12秒
震源からの距離が160km地点の2倍である320km地点では、初期微動継続時間も2倍になり、
午前7時25分19秒-午前7時24分55秒=24秒
になっています。
例えばここで、震源からの距離が480km地点での初期微動継続時間を求めよという問題が出された場合、比例式をつくって解きます。
160km:480km=12秒:x秒
x=36秒



コメント