【定期テスト対策問題】直列回路と並列回路の計算問題

回路と電流の最初の山、直列回路と並列回路の計算問題です。ここを乗り越えれば、電気計算が得意になります。頑張りましょう！

【練習問題❶】直列回路と並列回路

下の図のように、導線を接続し電流が流れる回路をつくった。これについて、次の各問いに答えよ。

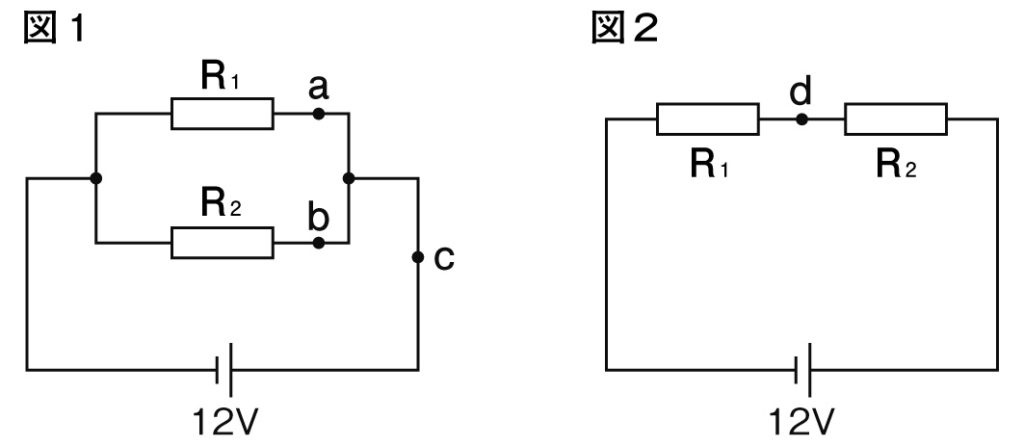
（1）図1のように、電流が流れる回路が枝分かれしている回路を何というか。

（2）図1の回路で、ａ点に1.2Ａ、ｃ点に3.0Ａの電流が流れているとき、ｂ点には何Ａの電流が流れているか。

（3）図1の回路で、電源の電圧が12Ｖのとき、R₁とR₂にはそれぞれ何Vの電圧がかかるか。それぞれ答えなさい。

（4）図2のように、電流が流れる回路が枝分かれしていない回路を何というか。

（5）図2の回路で、ｄ点に2.3Aの電流が流れているとき、電源には何Aの電流が流れているか。

（6）図2の回路で、電源の電圧が12Vのとき、R₁に5.0Vの電圧がかかっているとき、R₂には何Vの電圧がかかるか。

【解答・解説❶】回路と電流・電圧

（1）並列回路

電流が流れる回路が枝分かれしている回路を並列回路といいます。「並列」を「平列」と間違わないようにしましょう。

（2）1.8A

並列回路の場合、各抵抗に流れる電流の和が、電源に流れる電流と等しくなります。電源に流れる電流が3.0Aで、R₁に1.2Aの電流が流れているので、R₂には、3.0－1.2＝1.8Aの電流が流れています。

（3）R₁:12V　R₂:12V

並列回路の場合、回路にかかる電圧は、どこでも等しくなります。電源の電圧が12Vなので、各抵抗にも12Vの電圧がかかります。

（4）直列回路

電流が流れる回路が途中で枝分かれしていない回路を直列回路といいます。電圧計が並列に接続されていても直列回路になる点に注意しましょう。

（5）2.3A

直列回路の場合、電流が流れる道が1本しかないので、電流はどこでも同じになります。したがって、電源に流れる電流も2.3Aになります。

（6）7.0V

直列回路の場合、各抵抗にかかる電圧の和が電源の電圧と等しくなります。電源の電圧が12Vで、R₁に5.0Vの電圧がかかっているので、R₂には、12－5.0＝7.0Vの電圧がかかります

【練習問題❷】オームの法則と直列回路・並列回路の計算

下の図のような回路をつくり、電熱線Aと電熱線Bのそれぞれに加える電圧と流れる電流を測定した。グラフはその結果を表したものである。次の各問いに答えなさい。

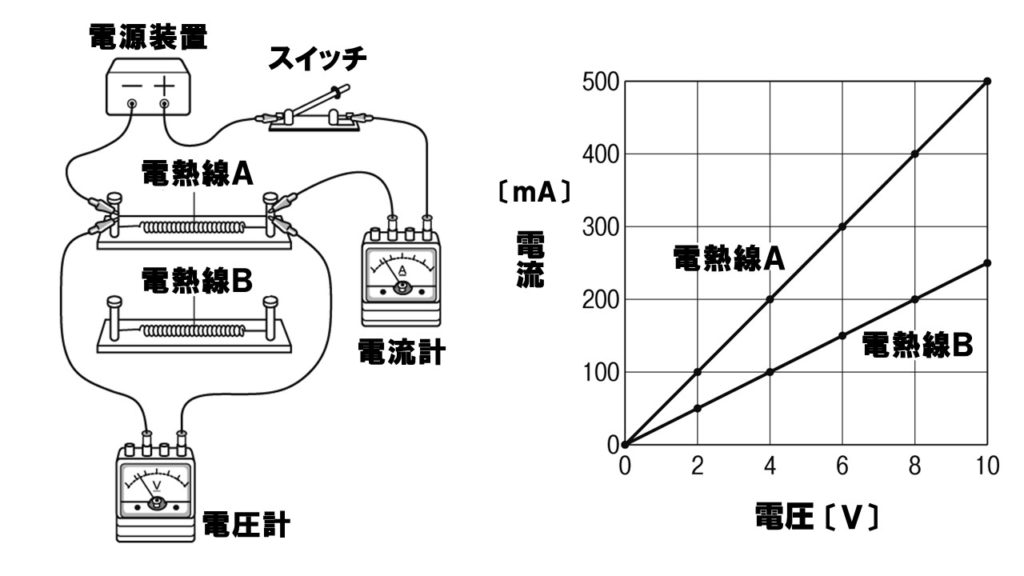
（1）グラフから、電熱線に加わる電圧と流れる電流との間には、何という関係があるとわかるか。

（2）（1）のことを何の法則というか。

（3）電熱線Aに6Vの電圧を加えた。このとき流れる電流は何Aか。

（4）電熱線Bの抵抗は電熱線Aの抵抗の何倍の大きさか。

（5）電熱線Aと電熱線Bを用いて直列回路をつくった。電源装置の電圧を12Vにしたとき、回路を流れる電流は何Aになるか。

（6）（5）のとき、電熱線Aには何Vの電圧がかかるか。

（7）（5）のとき、電熱線Bの消費電力は何Wになるか。

（8）電熱線Aと電熱線Bを用いて並列回路をつくった。電源装置の電圧を12Vにしたとき、回路全体を流れる電流は何Aになるか。

（9）（8）のときの回路全体の抵抗は何Ωか。四捨五入し整数で求めよ。

（10）（8）のとき回路全体で1分間に何Jの熱が発生するか。

【解答・解説❷】オームの法則と直列・並列回路の計算

（1）比例の関係
電流は流れる電気の大きさ、電圧は電流を流そうとする圧力の大きさなので、電圧を2倍にすると、電流も2倍になります。

（2）オームの法則
電熱線にかかる電圧と流れる電流が比例することをオームの法則といいます。

（3）0.3A
グラフから、電熱線Aに6Vの電圧がかかっているとき300mAの電流が流れています。1000mA＝1Aですので、300mAは0.3Aとなります。

（4）2倍
抵抗Ω＝電圧V÷電流Aで求めることができます。電熱線Aはグラフより2Vの電圧で100mAの電流が流れているので、2V÷0.1A＝20Ω。電熱線Bは4Vで100mAの電流が流れているので、4V÷0.1A＝40Ωとなります。したがって40Ω÷20Ωで2倍の大きさになります。

電流・電圧・抵抗の計算方法！次のテントウ虫で覚えておきましょう。

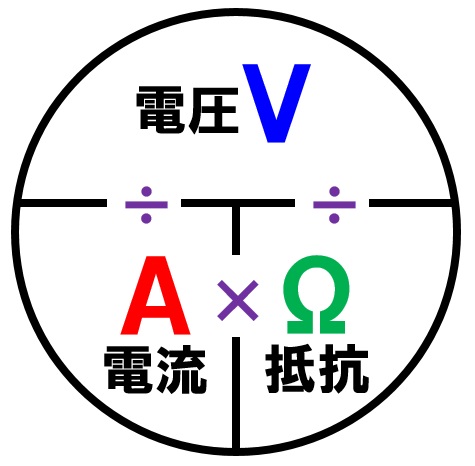
・電流［A］＝電圧［V］÷抵抗［Ω］
・電圧［V］＝電流［A］×抵抗［Ω］
・抵抗［Ω］＝電圧［V］÷電流［A］

（5）0.2A
直列回路の全体の抵抗は、各抵抗の和で求めることができるので20Ω＋40Ω＝60Ω。電源装置の電圧は12Vなので、12V÷60Ω＝0.2A。直列回路はどこも電流の大きさが等しいので答えは0.2Aになります。回路図を作成して、分かった数字を代入すると、次の回路図が完成します。

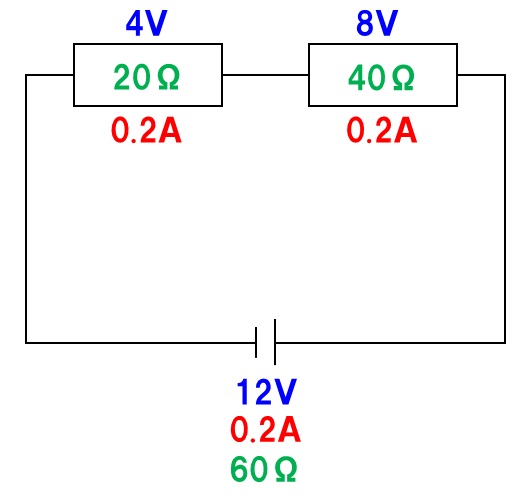
（6）4.0V
直列回路なので電熱線Aに流れる電流も0.2A。熱線Aの抵抗は20Ωなので、20Ω×0.2A＝4.0Vの電圧となります。

（7）1.6W
電力W＝電圧V×電流Aで求めることができます。電熱線Bの電圧8.0V。電流は0.2Aなので、8.0V×0.2A＝1.6Wとなります。

（8）0.9A
並列回路は電圧がどこでも等しく、電流は各抵抗を流れる電流の和が電源を流れる電流と等しくなります。電源装置の電圧が12Vなので、各抵抗にかかる電圧も12Vなので、電熱線Aを流れる電流は、12V÷20Ω＝0.6A、電熱線Bに流れる電流は、12V÷40Ω＝0.3A、回路全体を流れる電流は、0.6A＋0.3A＝0.9Aとなります。回路図を作成して、分かった数字を代入すると、次の回路図が完成します。

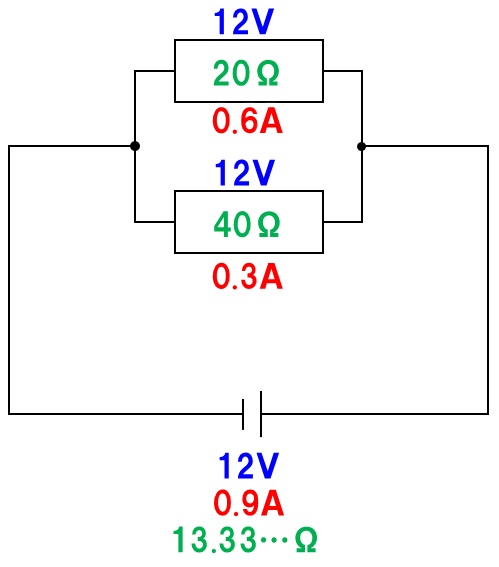
（9）13Ω
電源装置の電圧は12V、回路全体を流れる電流は0.9Aなので、回路全体の抵抗は12V÷0.9A＝13.33…したがって13Ωとなります。並列回路の全体の抵抗は、次のように「和」分の「積」で求めることもできます。

並列回路の全体の抵抗の求め方！「和」分の「積」でも求められます。

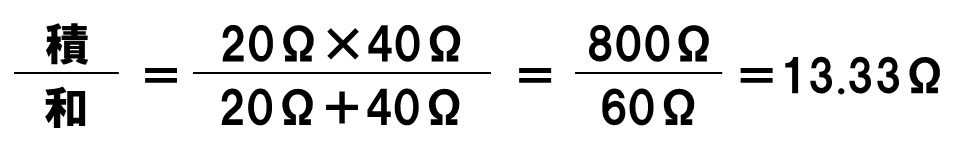
（10）648J
熱量J＝電力W×使用した秒sで求めることができます。回路全体の電圧は12V、電源を流れる電流が0.9Aなので、電力は12V×0.9A＝10.8W、1分間＝60秒なので、熱量Jは、10.8W×60s＝648Jとなります。