【中2理科】直列回路と並列回路の計算の仕方・練習問題

中学2年理科で学習する、電流と回路についてのまとめです直列回路と並列回路の特徴を理解し回路の計算ができるようになることが重要です。

回路と電流・電圧
1. 直列回路と電流・電圧
2. 並列回路と電流
直列回路の計算
1. 直列回路の練習問題
並列回路の計算
1. 並列回路の練習問題
【練習問題❶】直列回路と並列回路
1. 【解答・解説❶】回路と電流・電圧
【練習問題❷】オームの法則と直列回路・並列回路の計算
1. 【解答・解説❷】オームの法則と直列・並列回路の計算
【問題】回路と電流の一問一答
1. 【解答】回路と電流の一問一答

回路と電流・電圧

電流とは、電気の流れを表す量で、単位は［Ａ］アンペアを使いましたね。電圧とは、電流を流そうとする力（パワー）で、単位は［Ｖ］ボルトでした。大丈夫でしょうか。

次は、この電流と電圧が回路の中でどのような関係になっているのかを学習します。ここが理解できないと、これからの計算問題でつまづくことになります。ルールをしっかりと覚えて、この後の計算がスムーズにできるように頑張ってください。

直列回路と電流・電圧

直列回路とは、電流が流れる導線が途中で枝分かれしていない回路です。回路を流れる電流は、水の流れと同じようなものでしたね。したがって、直列回路の場合、流れる電流の大きさは、どこを測っても同じ大きさになります。電源を3.0Ａの電流が流れたのなら、回路に接続されている豆電球や抵抗器を流れる電流はどこも3.0Ａになります。

直列回路の電圧はどうなっているのでしょうか。電源の電池などには、電流を流すパワーである電圧を持っています。直列回路の場合、この電圧が回路に接続されている電流が流れにくいものである豆電球や電気器具などの抵抗に振り分けられます。言い方を変えると、各抵抗にかかっている電圧を足し合わせると、電源（全体）の電圧になるのです。

直列回路の電流・電圧❶直列回路の場合、電流の大きさ［Ａ］はどこでも同じ。
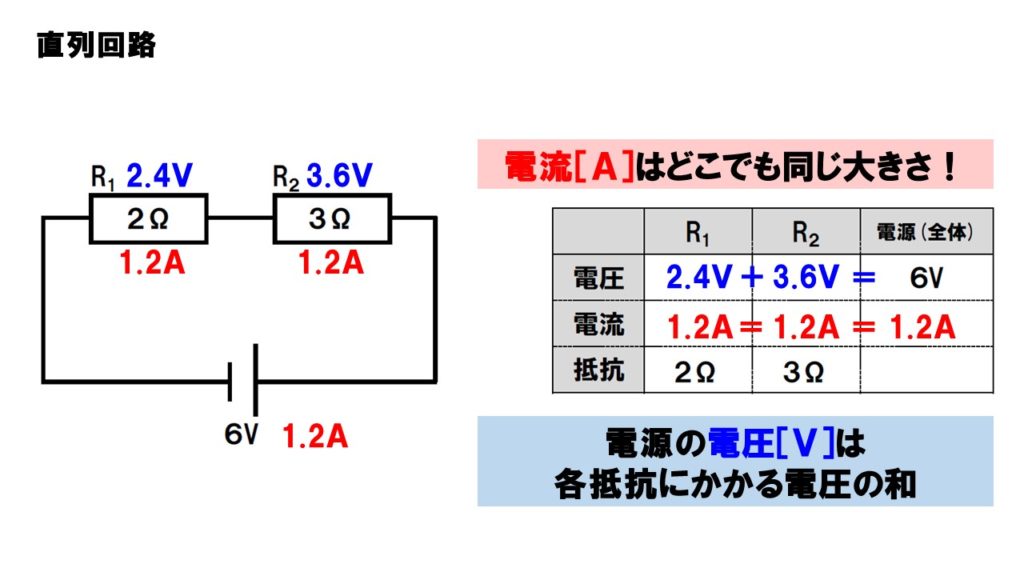
❷直列回路の場合、各抵抗にかかっている電圧の和が電源（全体）の電圧になる。

並列回路と電流

並列回路とは、電流が流れる電流が途中で枝分かれしている回路です。電流が流れる通路がわかれるのですから、各抵抗に流れる電流を足し合わせると、電源（全体）を流れる電流になります。例えば、電源から10Ａの電流が流れ、並列につながれている抵抗Ａに2Ａの電流が流れた場合、もう一つの抵抗Ｂには8Ａの電流が流れることになります。

電流を流そうとする力である電圧は、どこで測っても同じ値になります。電源の電圧が10Ｖの場合、どの抵抗にかかる電圧も10Ｖになるのです。

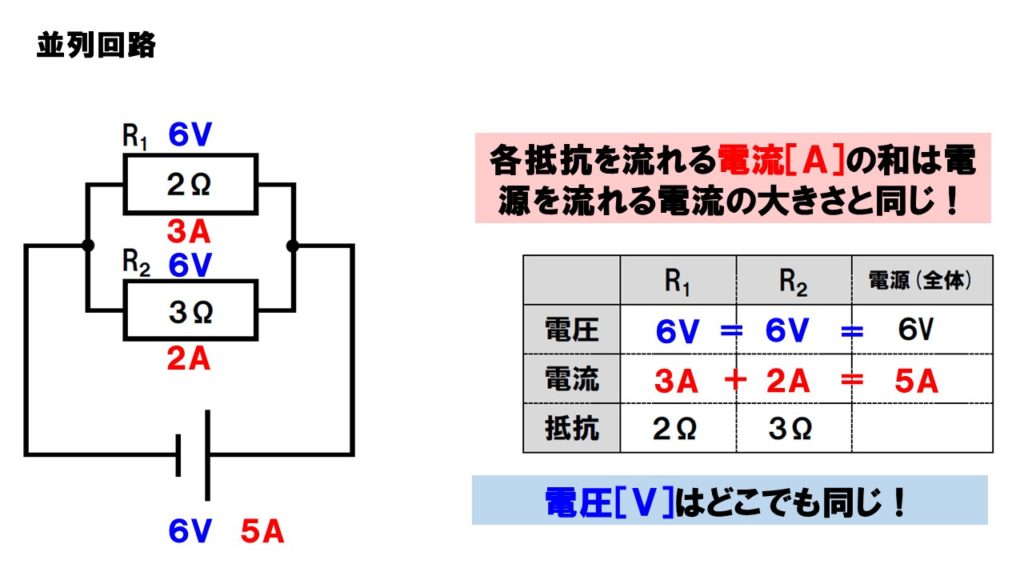
並列回路と電流・電圧❶並列回路の場合、各抵抗を流れる電流の和が電源（全体）の電流になる。
❷並列の場合、電圧はどこでも同じ大きさになる。

直列回路の計算

抵抗の大きさが40ΩのR1と、抵抗の大きさがわからないR2が直列に接続されており、電源の電圧が30Vで、R2に10Vの電圧が加わっている場合。

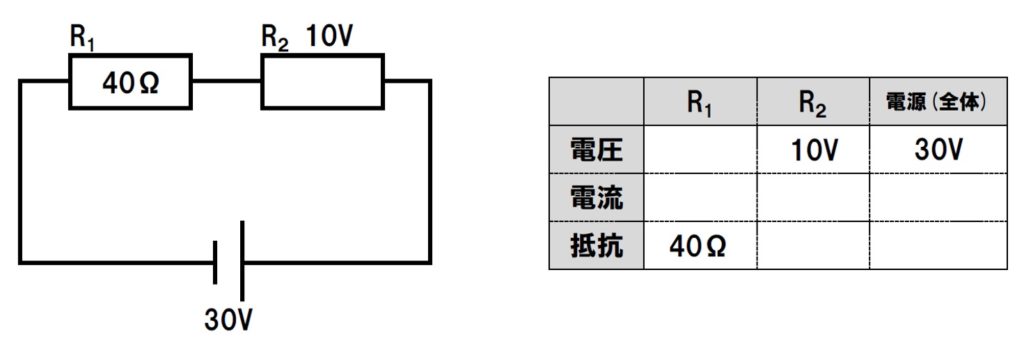
回路図にわかる数字をどんどん書き入れていきます。

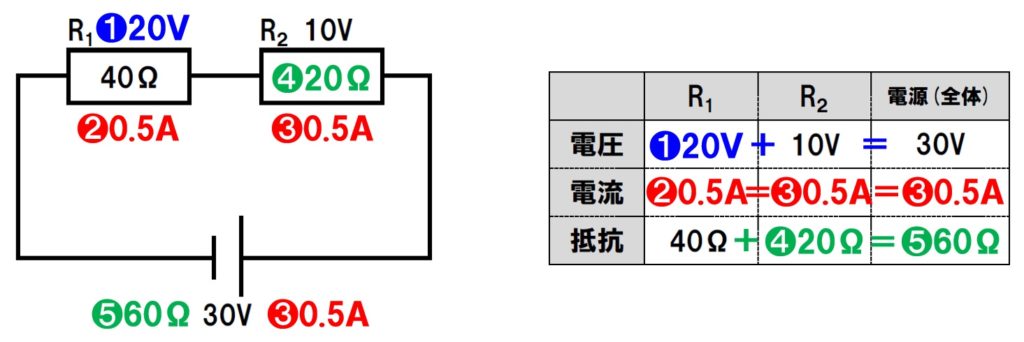
直列回路の場合、電源の電圧が各抵抗に振り分けられます。電源の電圧が30Vで、R2の電圧が10Vなので、
30V－10V＝20V
R1の抵抗が40Ω、R1にかかる電圧が20Vとわかったので、
20V÷40Ω＝0.5A
直列回路の電流はどこでも同じなので、
R2も電源も0.5A
R2にかかっている電圧が10V、電流の大きさが0.5Aとわかったので、
10V÷0.5A＝20Ω
直列回路の全体の抵抗の大きさは、各抵抗の大きさの和になります。R1が40Ω、R2の抵抗が20Ωなので、
40Ω＋20Ω＝60Ω
電源の電圧が30V、電流が0.5Aなので、
30V÷0.5A＝60Ω
と検算までできれば確実に正解できます。

直列回路の練習問題

類題に挑戦しましょう。抵抗の大きさが2ΩのR1と3ΩのR2が直列に接続され、電源の電圧が6Vの場合。

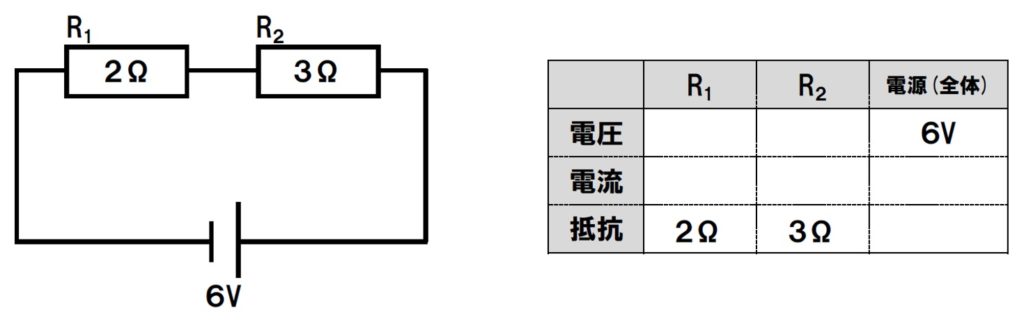
回路に流れる電流の大きさや、各抵抗にかかる電圧、全体の抵抗を求めてみよう。

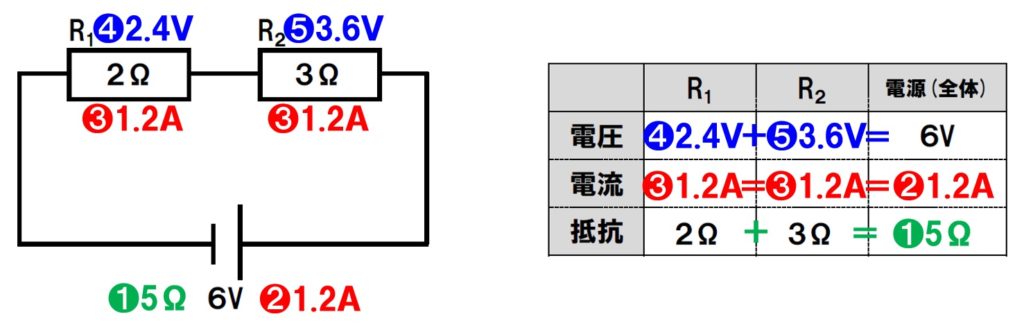
全体の抵抗
2Ω＋3Ω＝5Ω
電流の大きさ
6V÷5Ω＝1.2A
直列回路なので
全て1.2A
R1の電圧
2Ω×1.2A＝2.4V
R2の電圧
3Ω×1.2A＝3.6V

並列回路の計算

抵抗の大きさがわからないR1と、抵抗の大きさが10ΩのR2が並列に接続された回路がある。電源の電流が0.8A、R1に流れる電流が0.5Aの場合。

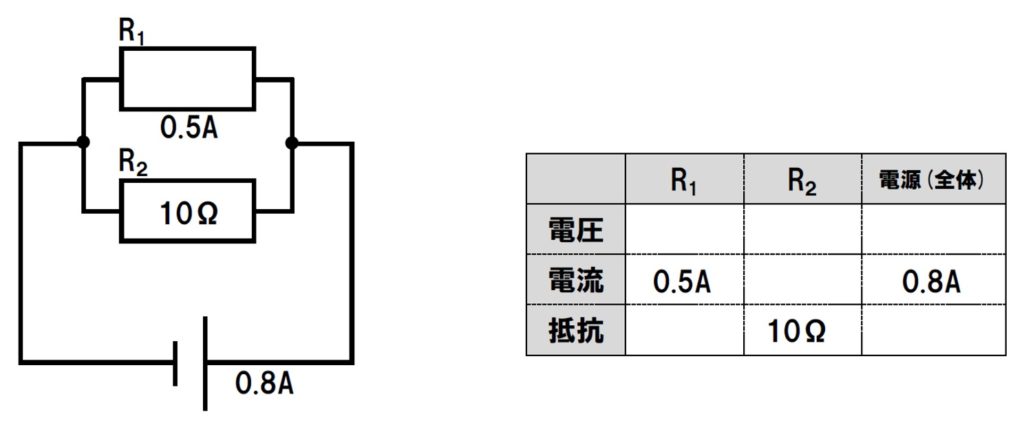
回路図にわかる数字をどんどん書き入れていきます。

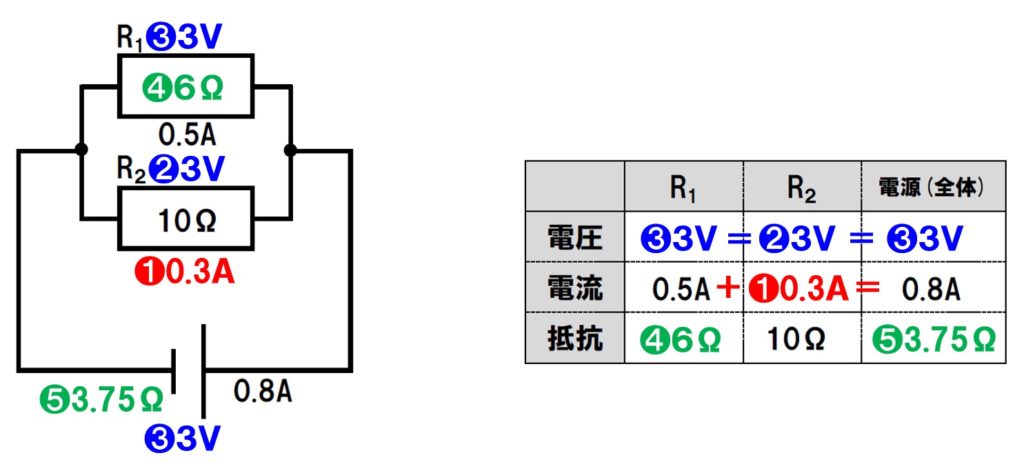
電源を流れる電流が枝分かれして流れるので、
0.8A－0.5A＝0.3A
R2の抵抗が10Ω、流れる電流が0.3Aなので、
10Ω×0.3A＝3V
並列回路の電圧はすべて等しいので、
全て3V
R1にかかる電圧が3V、電流が0.5Aなので、
3V÷0.5A＝6Ω
電源の電圧が3V、電源を流れる電流が0.8Aなので、
3V÷0.8A＝3.75Ω

並列回路の全体の抵抗は、各抵抗の和で求めることはできないので注意が必要です。電源の電圧と、電源を流れる電流から計算することになります。また、各抵抗の逆数の和が、全体の抵抗の逆数になることを利用して計算することもできます。下記の練習問題で並列回路の合成抵抗の求め方を紹介しています。

並列回路の練習問題

類題に挑戦しましょう。抵抗の大きさが2ΩのR1と、3ΩのR2が並列に接続されている。電源の電圧が6Vの場合。

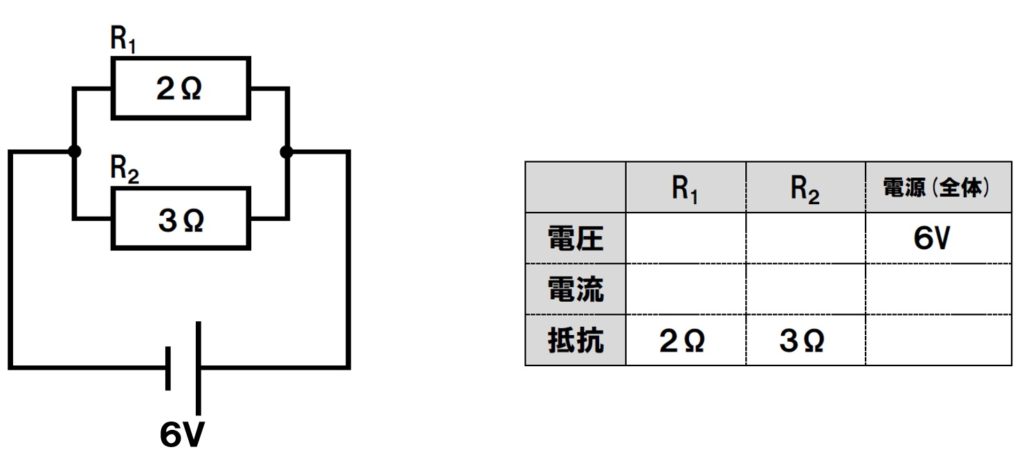
各抵抗にかかる電圧や、流れる電流、全体の抵抗まで求めてみよう。

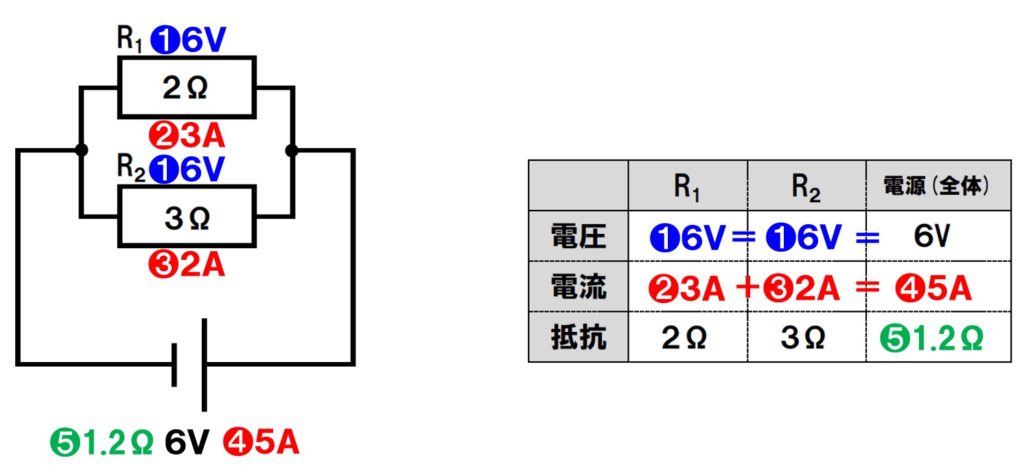
並列回路の電圧はどこでも同じなので、
全て6V
R1の抵抗は、
6V÷2Ω＝3A
R2の抵抗は、
6V÷3Ω＝2A
電源（全体）の電流
3A＋2A＝5A
全体の抵抗
6V÷5A＝1.2Ω

【練習問題❶】直列回路と並列回路

下の図のように、導線を接続し電流が流れる回路をつくった。これについて、次の各問いに答えよ。

（1）図1のように、電流が流れる回路が枝分かれしている回路を何というか。

（2）図1の回路で、ａ点に1.2Ａ、ｃ点に3.0Ａの電流が流れているとき、ｂ点には何Ａの電流が流れているか。

（3）図1の回路で、電源の電圧が12Ｖのとき、R₁とR₂にはそれぞれ何Vの電圧がかかるか。それぞれ答えなさい。

（4）図2のように、電流が流れる回路が枝分かれしていない回路を何というか。

（5）図2の回路で、ｄ点に2.3Aの電流が流れているとき、電源には何Aの電流が流れているか。

（6）図2の回路で、電源の電圧が12Vのとき、R₁に5.0Vの電圧がかかっているとき、R₂には何Vの電圧がかかるか。

【解答・解説❶】回路と電流・電圧

（1）並列回路

電流が流れる回路が枝分かれしている回路を並列回路といいます。「並列」を「平列」と間違わないようにしましょう。

（2）1.8A

並列回路の場合、各抵抗に流れる電流の和が、電源に流れる電流と等しくなります。電源に流れる電流が3.0Aで、R₁に1.2Aの電流が流れているので、R₂には、3.0－1.2＝1.8Aの電流が流れています。

（3）R₁:12V　R₂:12V

並列回路の場合、回路にかかる電圧は、どこでも等しくなります。電源の電圧が12Vなので、各抵抗にも12Vの電圧がかかります。

（4）直列回路

電流が流れる回路が途中で枝分かれしていない回路を直列回路といいます。電圧計が並列に接続されていても直列回路になる点に注意しましょう。

（5）2.3A

直列回路の場合、電流が流れる道が1本しかないので、電流はどこでも同じになります。したがって、電源に流れる電流も2.3Aになります。

（6）7.0V

直列回路の場合、各抵抗にかかる電圧の和が電源の電圧と等しくなります。電源の電圧が12Vで、R₁に5.0Vの電圧がかかっているので、R₂には、12－5.0＝7.0Vの電圧がかかります

【練習問題❷】オームの法則と直列回路・並列回路の計算

下の図のような回路をつくり、電熱線Aと電熱線Bのそれぞれに加える電圧と流れる電流を測定した。グラフはその結果を表したものである。次の各問いに答えなさい。

（1）グラフから、電熱線に加わる電圧と流れる電流との間には、何という関係があるとわかるか。

（2）（1）のことを何の法則というか。

（3）電熱線Aに6Vの電圧を加えた。このとき流れる電流は何Aか。

（4）電熱線Bの抵抗は電熱線Aの抵抗の何倍の大きさか。

（5）電熱線Aと電熱線Bを用いて直列回路をつくった。電源装置の電圧を12Vにしたとき、回路を流れる電流は何Aになるか。

（6）（5）のとき、電熱線Aには何Vの電圧がかかるか。

（7）（5）のとき、電熱線Bの消費電力は何Wになるか。

（8）電熱線Aと電熱線Bを用いて並列回路をつくった。電源装置の電圧を12Vにしたとき、回路全体を流れる電流は何Aになるか。

（9）（8）のときの回路全体の抵抗は何Ωか。四捨五入し整数で求めよ。

（10）（8）のとき回路全体で1分間に何Jの熱が発生するか。

【解答・解説❷】オームの法則と直列・並列回路の計算

（1）比例の関係
電流は流れる電気の大きさ、電圧は電流を流そうとする圧力の大きさなので、電圧を2倍にすると、電流も2倍になります。

（2）オームの法則
電熱線にかかる電圧と流れる電流が比例することをオームの法則といいます。

（3）0.3A
グラフから、電熱線Aに6Vの電圧がかかっているとき300mAの電流が流れています。1000mA＝1Aですので、300mAは0.3Aとなります。

（4）2倍
抵抗Ω＝電圧V÷電流Aで求めることができます。電熱線Aはグラフより2Vの電圧で100mAの電流が流れているので、2V÷0.1A＝20Ω。電熱線Bは4Vで100mAの電流が流れているので、4V÷0.1A＝40Ωとなります。したがって40Ω÷20Ωで2倍の大きさになります。

電流・電圧・抵抗の計算方法！次のテントウ虫で覚えておきましょう。

・電流［A］＝電圧［V］÷抵抗［Ω］
・電圧［V］＝電流［A］×抵抗［Ω］
・抵抗［Ω］＝電圧［V］÷電流［A］

（5）0.2A
直列回路の全体の抵抗は、各抵抗の和で求めることができるので20Ω＋40Ω＝60Ω。電源装置の電圧は12Vなので、12V÷60Ω＝0.2A。直列回路はどこも電流の大きさが等しいので答えは0.2Aになります。回路図を作成して、分かった数字を代入すると、次の回路図が完成します。

（6）4.0V
直列回路なので電熱線Aに流れる電流も0.2A。熱線Aの抵抗は20Ωなので、20Ω×0.2A＝4.0Vの電圧となります。

（7）1.6W
電力W＝電圧V×電流Aで求めることができます。電熱線Bの電圧8.0V。電流は0.2Aなので、8.0V×0.2A＝1.6Wとなります。

電力［W］の求め方！電力［W］は電圧と電流の積で求めます。
電力［W］＝電圧［V］×電流［A］

（8）0.9A
並列回路は電圧がどこでも等しく、電流は各抵抗を流れる電流の和が電源を流れる電流と等しくなります。電源装置の電圧が12Vなので、各抵抗にかかる電圧も12Vなので、電熱線Aを流れる電流は、12V÷20Ω＝0.6A、電熱線Bに流れる電流は、12V÷40Ω＝0.3A、回路全体を流れる電流は、0.6A＋0.3A＝0.9Aとなります。回路図を作成して、分かった数字を代入すると、次の回路図が完成します。