円周角を求める問題の出題パターンとその解き方です。
円周角の出題パターン
円周角を求めさせる問題は、高校入試では、ほぼ100%出題されるといって過言でない単元です。その理由として多くの解法パターンがあること、中学生で習った図形の角についての性質を知っているかを確認することができるからでしょう。1つ1つしっかりおさえていきましょう。それでは、円周角を求める問題の出題パターンとその解き方です。
同じ弧に対する円周角
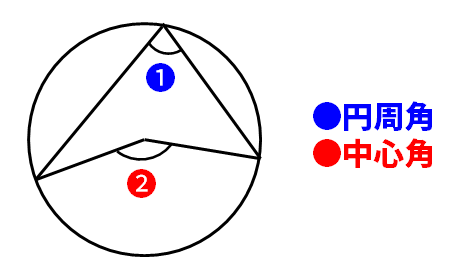
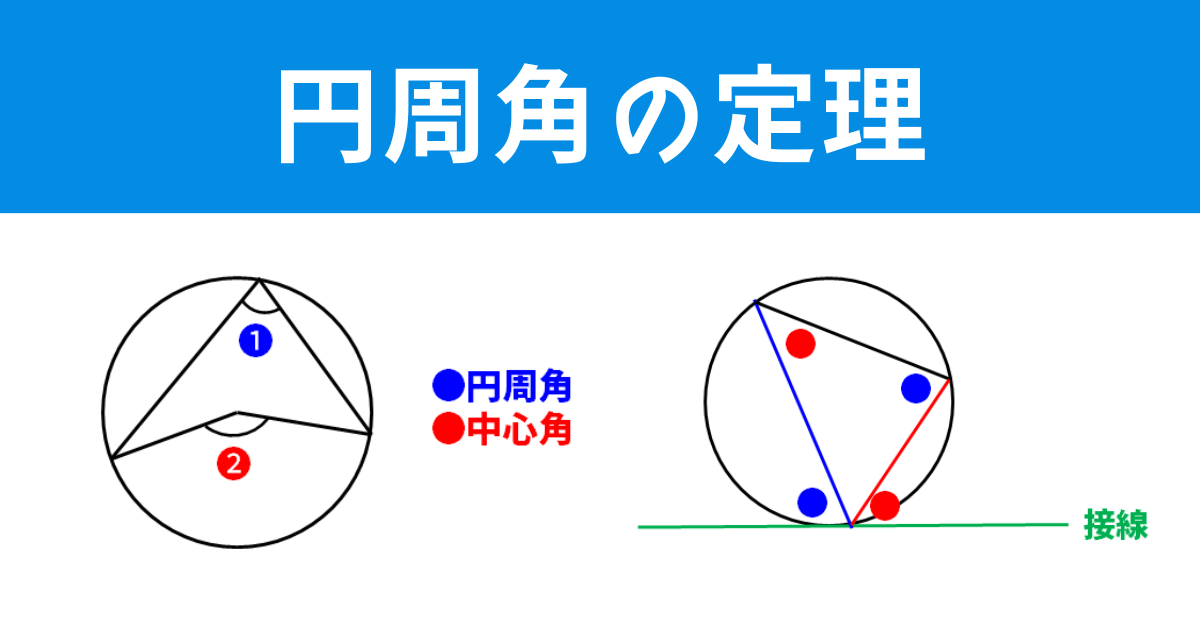
(公式)円周角=中心角×1/2(円周角は中心角の半分の大きさ)
(注意点)弧の長さが長いとき、円周角は鈍角(90°以上)になるときに注意
円周角と弧の長さの関係
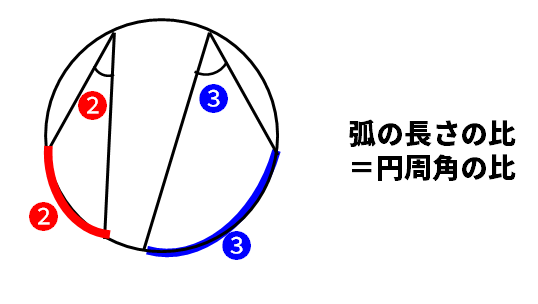
(公式)円周角は弧の長さに比例
(ポイント)弧Aの長さ:弧Bの長さ=円周角A:円周角B
内接する四角形の定理
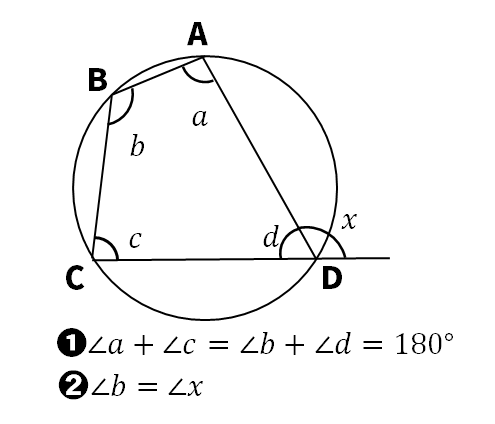
(公式1)向かい合う角の和は180°
(公式2)向かい合う角と隣り合う角と等しい
接弦定理
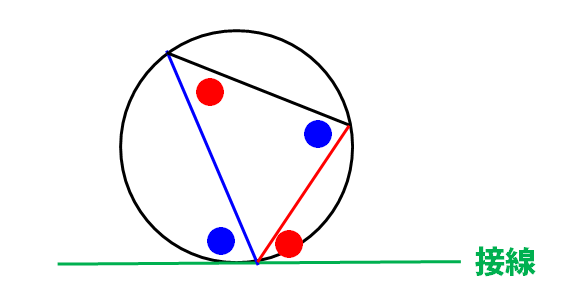
(公式)ある1つの弦と接線がつくる角は、その弦の円周角に等しい
半径と弦が作る角との関係
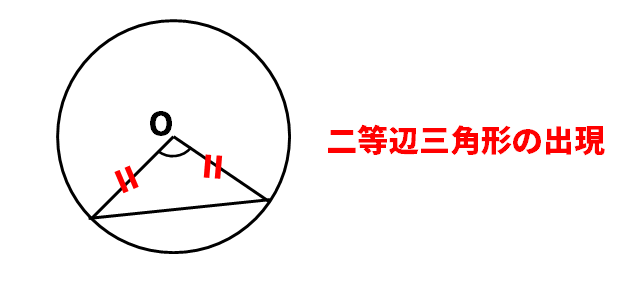
(公式)半径が等しいので、二等辺三角形が現れる
(性質)二等辺三角形より底角が等しい
(ポイント)円の中には、二等辺三角形が隠れている場合が多い。
円内の正三角形
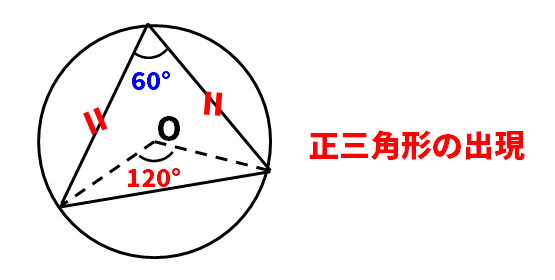
(公式)円周角60°、中心角120°の場合、正三角形出現
(ポイント)円の中には、正三角形が隠れている場合が多い。
直径と円周角の関係
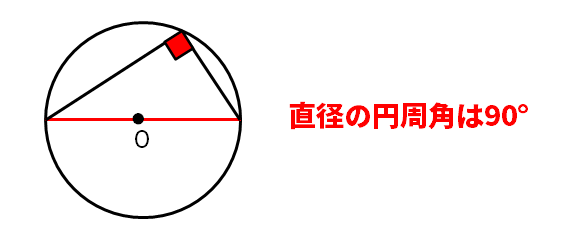
(公式)直径の円周角は90°
(ポイント)直径があり、90°が見つからない場合は、1本補助線を入れると90°ができる。
同じ弧から発生する円周角
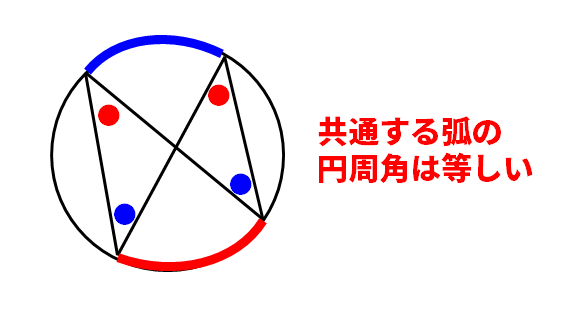
(公式)同じ弧から発生する円周角は等しい
(ポイント)円の中に、「ちょうちょ」があると利用する場合が多い。
角度を求める問題の注意点
そのほか
- 三角形の外角の定理
- 平行であれば、錯覚は等しい
- 平行であれば、同位角は等しい
- 対頂角は等しい
など、これまで習ってきた図形の性質を総動員して解いていきましょう。









コメント