【中学数学二次関数】正方形になるときの座標を求める問題

【中学数学二次関数】正方形になるときの座標を求める問題です。

【問題】正方形になるときの座標を求める問題（中学数学）

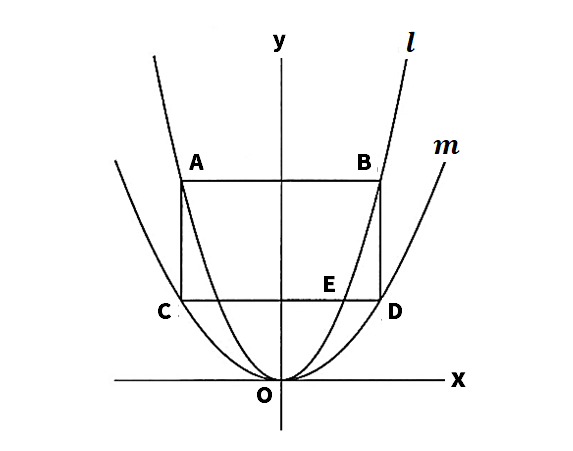
次の図で、曲線lは関数y=x²、曲線mは関数y=ax²(0<a<1)のグラフである。2点A、Bはl上の点で、そのy座標は等しく、点Aのx座標は負である。また、AB=CD、AB//CDとなるように2点C、Dを上にとる。さらに、線分CDとlとの交点のうち、x座標が正であるものを点Eとする。これについて、次の問いに答えなさい。

(1)a=1/3のとき、次の問いに答えなさい。
➀：点Aのx座標が-6のとき、点Eの座標を求めなさい。
➁：四角形ACDBが正方形のとき、点Aの座標を求めなさい。

(2)CE:ED=3:1のとき、aの値を求めなさい。

【解答・解説】正方形になるときの座標を求める問題（中学数学）

(1)➀D(2√3,12)
AB=CD、AB//CD、y軸について、点Aと点B、点Cと点Dがそれぞれ対称だから、四角形ACDBは長方形である。点Aと点Cのx座標はともに-6で、点Cは放物線上の点だから、y=1/3x²にx=-6を代入して、C(-6、12)。点Cと点Eのy座標はともに12で、点Eは放物線l上の点だから、y=x²にy=12を代入して、x座標は正だから、E(2√3,12)。

(1)➁(-3,9)
点Aのx座標をt(t<0)とすると、A(t,t²)、B(-t,t²)と表せるから、AB=-t-t=-2t。また、点Cのx座標もだから、C(t,1/3t²)と表せるので、AC=2/3t²

四角形ACDBが正方形であるとき、AB=ACより2=1/3t²、これを解くとt=0、-3。t<0だから、t=-3。したがって、A(-3,9)。

(2)a=1/4
線分CDとy軸との交点をFとすると、CE:ED=3:1のとき、CF:FE:ED=2:1:1となるから、点Eのx座標をとおくと、点Dのx座標は2sと表せる。このとき、E(s,s²)、D(2s,4as²)と表すことができ、点Eと点Dのy座標は等しいので、s²=4as²これを解くとa=1/4