【高校受験対策数学】相似比を使って面積を求める練習問題

【高校受験対策数学】相似比を使って面積を求める練習問題です。

【問題】相似比を使って面積を求める練習問題

次の図で、四角形ABCDは正方形であり、Eは辺BC上の点で、BE:EC=1:3である。また、F、Gはそれぞれ線分DBとAE、ACとの交点である。AB=10cmのとき、次の問いに答えよ。

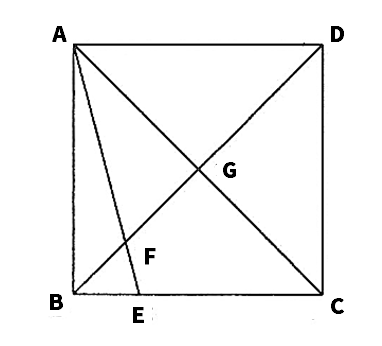
（1）△ADFと△EBFが相似であることを証明しなさい。

（2）線分FEの長さは線分AFの長さの何倍か求めなさい。

（3）△AFGの面積を求めよ。

（1）△ADFと△EBFにおいて
四角形ABCDは正方形なのでAD//BCより錯角は等しいので
∠ADF＝∠EBF…➀
∠DAF＝∠BEF…➁
➀➁より2つの角がそれぞれ等しいので
△ADF∽△EBF

（2）1/4倍
△EFBと△AFDで、AD//BE、
FE:AF=BE:AD=BE:BC=1:4
よって、1/4倍。

(3)15cm²
△ΑΒΕ=1/4×△АВС＝25/2
△ABF＝4/5×△ABE＝10
△AFG＝△ABG-△ABF＝1/4×10×10-10＝15(cm²)