中2数学の「二等辺三角形」についてまとめています。二等辺三角形に関して、定義・定理、証明、角度を求める問題までふれています。それでは、中2数学の「二等辺三角形」をみていきましょう。
二等辺三角形の定義
定義とは、使う言葉の意味をはっきり述べているものです。
二等辺三角形の性質
AB=ACである二等辺三角形ABCで等しい辺のつくる∠Aを頂角、頂角に対する辺BCを底辺、底辺の両端の角∠B、∠Cを底角といいます。
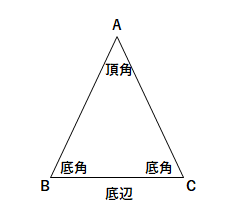
二等辺三角形
- 二等辺三角形の2つの底角は等しい。
二等辺三角形の頂角の二等分線
二等辺三角形の頂角の二等分線は、底辺を垂直に2等分します。
二等辺三角形の定理
定理とは、証明されたことがらのうち、基本になるものです。
- 二等辺三角形の2つの底角は等しい。
- 二等辺三角形の頂角の二等分線は、底辺を垂直に2等分する。
2つの角が等しい三角形は、二等辺三角形であるといえます。
底辺を垂直に2等分する証明
AB=ACの二等辺三角形ABCで、底辺BCの中点をMとすると、線分AMは∠Aを2等分することの証明です。
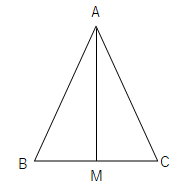
△ABMと△ACMで
仮定より、AB=AC …①
仮定より BM=CM …②
AMは、共通だから AM=AM …③
①②③より 3辺がそれぞれ等しいので、△ABM≡△ACM
合同な図形では対応する角は等しいので、∠BAM=∠CAM
したがて、線分AMは∠Aを2等分します。
【練習問題】二等辺三角形
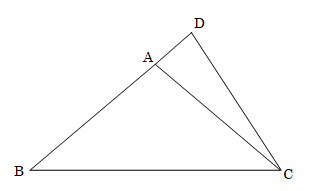
【問1】AB=ACであり、頂角∠BACが鈍角である二等辺三角形ABCがある。下の図のように、辺BAの延長線上にCA=CDとなる点Dをとる。∠ACD=16°のとき、∠ABCを求めなさい。
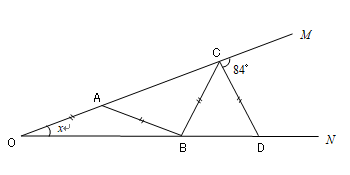
【問2】次の図の∠x の大きさを求めなさい。(OA=AB=BC=CD)
【問3】△ABCで、∠B=∠Cとすると、△ABCはAB=ACの二等辺三角形となることを証明せよ。

【解答】二等辺三角形
【問1】41°
【問2】21°
【問3】
∠Aの二等分線をひき、BCとの交点をDとします。
△AMBと△AMCで
仮定より、∠ABM=∠ACM …①
仮定より ∠BAM=∠CAM …②
三角形の3つの内角の和が180°であることと①②より
∠AMC=∠AMC…③
共通な辺より AM=AM…④
②③④より 1組の辺とその両端の角がそれぞれ等しいので、
△AMB≡△AMC
合同な図形では、対応する辺は等しいので。
AB=AC


コメント