【高校入試対策数学】三角形の重心に関する演習問題

【高校入試対策数学】三角形の重心に関する演習問題です。高校入試数学の中でも、図形問題は得点の鍵を握る重要な単元です。その中で「三角形の重心」は、理解すれば解きやすい一方で、仕組みをきちんと押さえていないと混乱しがちなテーマの一つです。三角形の重心とは、3本の中線（各辺の中点と対角の頂点を結ぶ線）が交わる一点で、常に各中線を 2:1 に内分する位置にあります。この特性を理解すると、図形の性質や応用問題で大いに役立ちます。

本記事では、三角形の重心に関する基礎的な知識から、実際の入試で出題されやすい演習問題までを解説します。重心の性質をしっかり押さえて、得点力をアップさせましょう！

三角形の重心の演習問題

次の△ABCの中線（三角形の頂点をそれに対する辺とを結ぶ線）ALとCMの交点をGとし、Mからひいた辺BCに平行な直線とALとの交点をNとする。BC=20cm,AL=12cmのとき、次の線分を求めなさい。

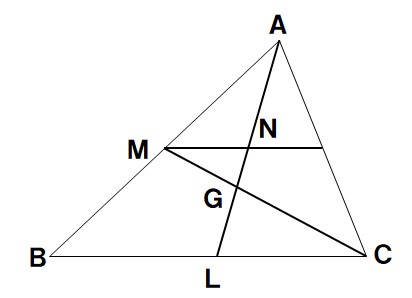
（1）MNの長さを求めなさい。

（2）NGの長さを求めなさい。

三角形の重心の演習問題解答

(1)MN=5cm
BL=10cm、中点連結定理より、MN=5cm

中点連結定理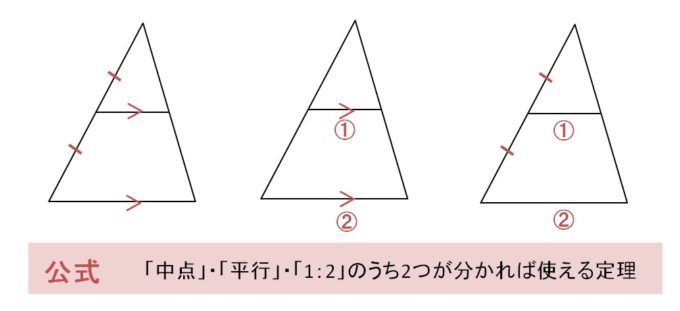

(2)NG＝2cm
三角形の重心より、GL=AL×1/3＝4cm
△MNG∽△CLG
MN:CL=NG:GL
5：10＝x：4
x＝2

三角形の重心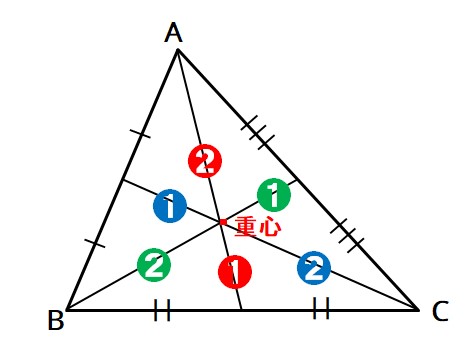
三角形の重心は、3つの中線それぞれを2：1に内分する。中線は、三角形の頂点からその対辺の中点を結んだ線のこと。