【中2数学】図形の角度を求める対策問題です。三角形の内角と外角、平行線の同位角や錯角についての基本的な性質を確認する問題です。
平行四辺形の角度の問題では、対角の大きさが等しいこと、となり合う角の和が180°であることを状況に合わせて使えるようにしましょう。
【問題】図形の角度を求める対策問題(中2数学)
【1】三角形と角
次の図で、∠xの大きさを求めなさい。
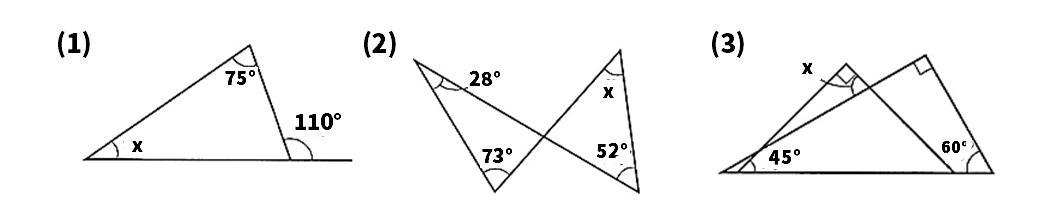
【2】平行線と角
次の図で、l//mのとき、xの大きさを求めなさい。
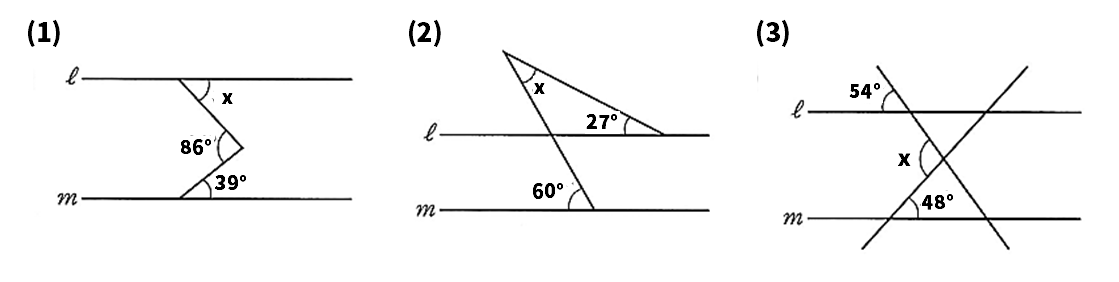
【3】図形と角
次の図で、∠xの大きさを求めなさい。ただし、同じ印の辺の長さ、角の大きさはそれぞれ等しいものとする。
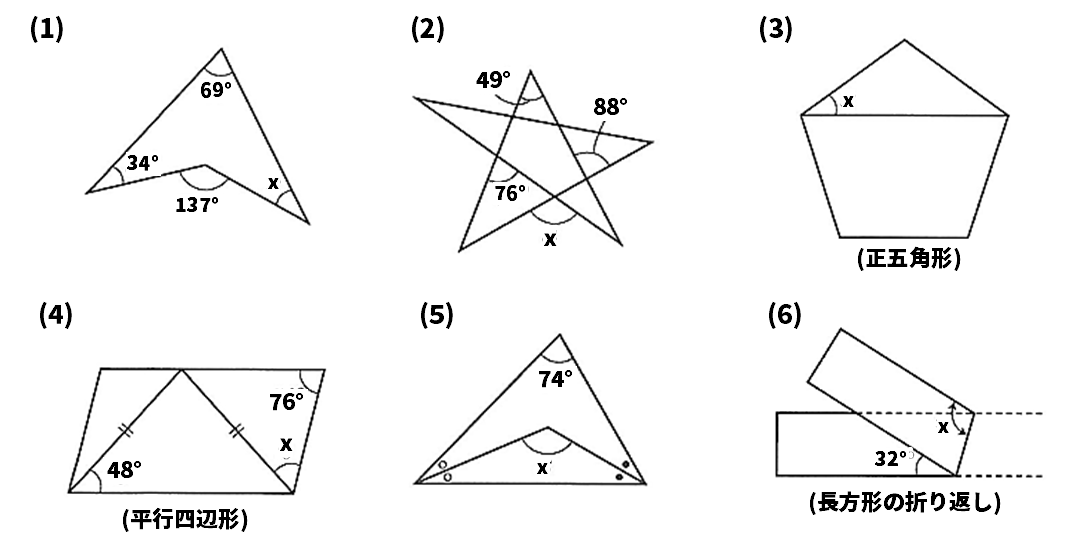
【解答・解説】図形の角度を求める対策問題(中2数学)
【1】三角形と角
(1)35°
三角形の外角は、それととなり合わない2つの内角の和に等しいことから、∠x+75°=110°、∠x=35°。
(2)49°
2つの三角形に共通な外角について、28+73°=∠x+52°、<x=101°-52°=49°。
(3)75°
∠ABC=180°-(90°+60°)=30°、∠DFE=180°-(90°+45°)=45°.∠BFGで、x=30°+45°=75°。
【2】平行線と角
(1)47°
86°の角の頂点を通り、lに平行な直線nをひき、∠x=39°の角の錯角をつくると、∠x+39=86°。これを解くとx=47°。
(2)33°
60°の角の同位角に着目すると、∠x+27°=60°。これを解くと∠x=33°
(3)102°
54°の角の同位角に着目すると、∠x=48°+54°=102°
【3】図形と角
(1)34°
点Eは線分BCの延長と線分ADの交点である。△ABEで、∠BED=69°+34°=103°だから、△CDEで、∠x+103°=137°これを解くとx=34°。
(2)115°
△ABCで、49°+∠B=88°、∠B=39°、△BEDで、∠x=76°+39°=115°。
(3)36°
△ABCは、AB=ACの二等辺三角形である。∠Aは正五角形の内角だから、∠A=180°×(5-2)÷5=108°。よって、∠x=(180°-108°)÷2=36°。
(4)56°
平行四辺形ABCDで、となり合う角の和は180°だから、∠BCD+76°=180°、∠BCD=104°。また、△EBCはEB=ECの二等辺三角形だから、∠ECB=∠EBC=48°。よって、x=104°-48°=56°。
(5)127°
○印をつけた角をa、・印をつけた角をbとすると、△ABCで、74°+2a+2b=180°、2(a+b)=106°、a+b=53°。△DBCで、∠x+a+b=180°、∠x=180°-53°=127°。
(6)106°
∠ABC=∠DBC、∠ABC=(180°−32°)÷2=74°。AE//BDより錯角は等しいから、∠BCE=32°+74°=106°。よって、∠x=∠BCE=106°。


コメント