【中2数学】一次関数の利用問題（速さ・すれ違った時間を求める問題）です。
【問題】速さ・すれ違った時間を求める問題（一次関数利用）
学校から図書館までは、まっすぐな道路上で1200m離れており、その途中に公園がある。P君は17時ちょうどに学校を出発し毎分一定の速さで走って公園に向かった。公園で休憩をした後、最初と同じ速さで走り、図書館に着いた。右の図は、P君が学校を出発してからの時間をx分、P君の学校からの距離をymとして、xとyの関係をグラフに表したものである。これについて、次の問いに答えなさい。
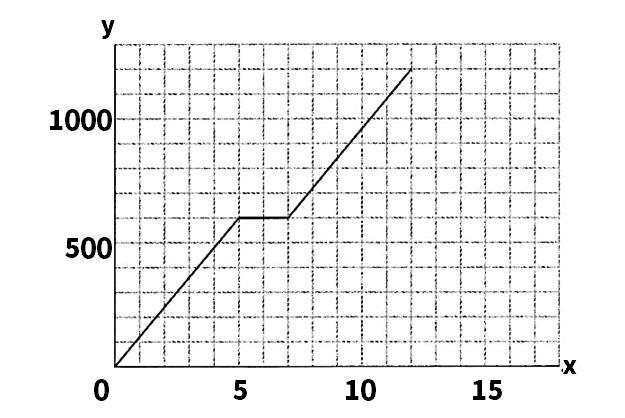
（1）P君の走る速さは、毎分何mですか。
（2）Q君は17時2分に図書館を出発し、毎分80mの速さで歩いて学校へ向かったところ、途中でP君とすれ違った。Q君は公園等で休憩せずに歩き続けたとして、次の問いに答えなさい。
ア：Q君の移動を表すグラフを図にかきなさい。
イ：Q君がP君とすれ違ったのは、学校から何m離れた地点ですか。
【解答・解説】速さ・すれ違った時間を求める問題（一次関数利用）
（1）毎分120m
グラフより、学校から公園までの道のりは600mで、P君はこの道のりを進むのに、5分かかっていることがわかる。よって、P君の走る速さは、600÷5=120(m/分)。
（2）ア：図参照イ：720m
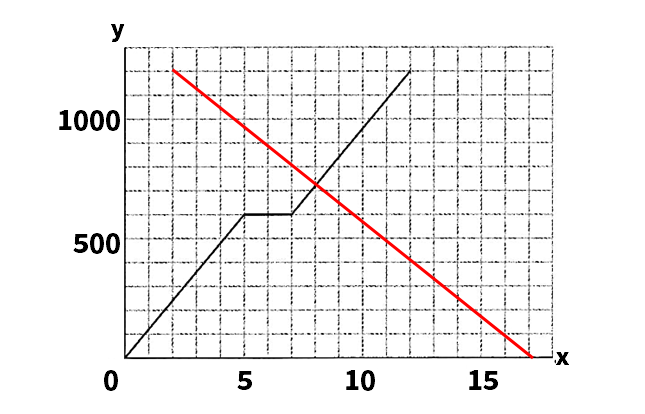
ア：Q君の歩く速さは毎分80mだから、図書館から学校までは、1200÷80=15(分)より、15分かかることがわかる。よって、Q君が学校に着いたのは、17時2分+15分=17時17分。したがって、Q君の移動を表すグラフは、2点(2,1200)、(17,0)を結んだ直線となる。
イ：公園で休憩した後のP君の移動を表すグラフは2点(7,600)、(12,1200)を結んだ直線で、その式はy=120x-240(7≦x≦12)…（a）
また、イでかいたQ君の移動を表すグラフの式は、y=-80x+1360(2≦x≦17)…（b）
(a)、(b)を連立方程式として解くと、x=8、y=720。
したがって、Q君がP君とすれ違ったのは、学校から720m離れた地点である。
コメント