【中学数学二次関数】台形の面積を二等分する直線の式を求める練習問題

【中学数学二次関数】台形の面積を二等分する直線の式を求める練習問題です、

【問題】台形の面積を二等分する直線の式を求める練習問題

次の図において、➀は関数y=x²、➁は1次関数y=-x+12のグラフである。A(2,4)は➀のグラフ上の点、B(2,10)は➁のグラフ上の点である。Cは➀のグラフ上を動く点、Dは➁のグラフ上を動く点で、CとDのx座標は等しいものとする。

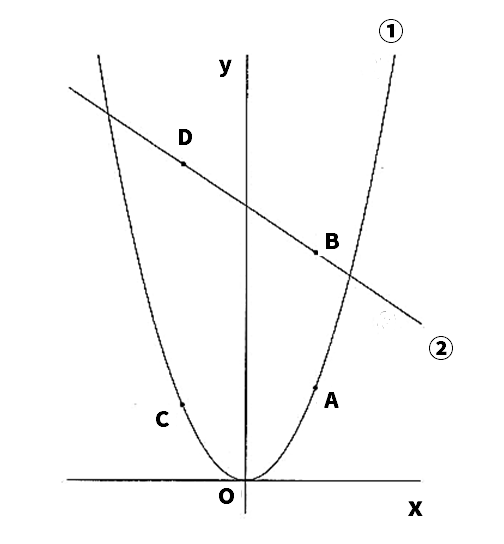
(1)➀の関数y=x²について、xの変域が−2≦x≦4のときyの変域を求めよ。

(2)四角形ABDCが平行四辺形となるとき、点Cの座標を求めよ。

(3)2点C,Dのx座標がともに-1のとき、点Aを通り、四角形ABDCの面積を2等分する直線ℓの式を求めよ。

(1)0≦y≦16

(2)(-3,9)
点Cの座標を(t,t²⁾とおく。
点Dの座標は、x=t、y=-t+12
四角形ABDCは平行四辺形だから、
DC=ABより、
(t−2)(t+3)=0
t<0より、t=-3

(3)y=-2x+8
C,D座標は、C(-1,1),D(-1,13)。求める直線とCDの交点をE(-1,p)とする。
△ACEと四角形ABDEの面積が等しいから、
DE+BA＝CE
13-p+(10-4)=p-1
これを解いて、p=10
2点(-1,10)、(2,4)を通る直線の式を求める。