【中学数学二次関数】面積が等しくなる座標を求める等積変形の問題

【中学数学二次関数】面積が等しくなる座標を求める等積変形の問題です。

【問題】面積が等しくなる座標を求める等積変形の問題（中学関数）

次の図のように、関数y=1/4x²…➀のグラフ上に2点A、Bがあり、点Aのx座標は-4、点Bのx座標は8である。また、点Pは1のグラフ上のAからBまでの部分にある点である。座標軸の1目もりを1cmとして、次の問いに答えなさい。

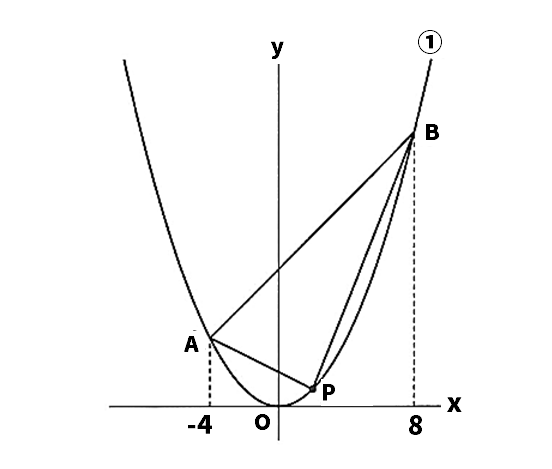
(1)点Pのx座標が2のとき、△APBの面積を求めなさい。
(2)△APBの面積が30cm²のとき、点Pの座標をすべて求めなさい。

(1)54cm²
（下準備）
y=1/4x²にx=-4を代入して、A(-4,4)。y=1/4²にx=8を代入して、B(8,16)。これより、2点A、Bを通る直線の式を求めると、y=x+8…➁

直線➁上にあり、x座標が2である点をQとするとy=x+8にx=2を代入して、y=2+8=10より、Q(2,10)。また、点Pのy座標は、y=1/4²にx=2を代入して、P(2,1)。よって、PQ=10-1=9(cm)。したがって、△APB=△APQ+△BPQ=54(cm²)。

(2)(-2,1)、(6,9)
点Pのx座標をpとすると、P(p,1/4p²)と表せる。また、直線➁上にあり、x座標がpである点をSとすると、S(p,p+8)と表せるから、PS=-1/4p²+p+8(cm).

(1)と同じように考えると、△APB=1/2×PS×12=-3/2p²+6p+48(cm)。△APB=30cm²となるとき、-3/2p²+6p+48=30より、p=-2,6。これらはともに、-4≦p≦8を満たすから、p=-2のとき、P(-2,1)、p=6のとき、P(6,9)。