【中2数学】図形の合同の証明の対策問題

【中2数学】図形の合同の証明の対策問題です。

2つの三角形が「合同である」ことを証明するためには、その2つの三角形が「合同条件を満たす」ことが必要があります。なので、「合同条件に必要な等しい辺や角」を見つけ、「その辺や角が等しくなる根拠」を整理することが大切です。

コツとしては、証明する図形の組を最後の結論を決定して、記述していくといいでしょう。

【問題】図形の合同の証明（中2数学）

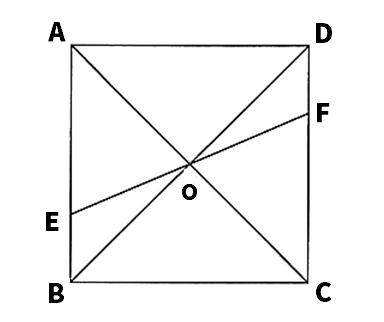
【1】次の図のように、正方形ABCDの対角線の交点をOとする。辺AB上に点Eをとり、直線EOと辺CDとの交点をFとするとき、△EBOと△FDOが合同であることを証明をしなさい。

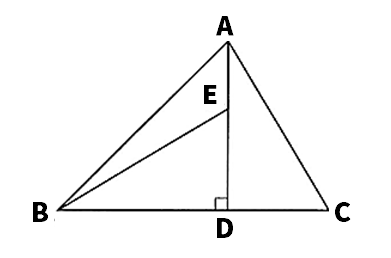
【2】次の図のように、∠ABC=45°である△ABCがある。頂点Aから辺BCにひいた垂線と辺BCとの交点をDとし、線分AD上に、DC=DEとなる点Eをとり、点Bと点Eを結ぶ。このとき、△ADC≡△BDEであることを証明しなさい。

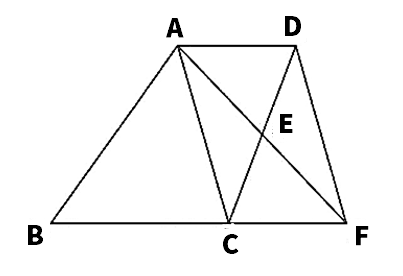
【3】次の図の正三角形ABCで、辺BC、AC上にそれぞれ点D、Eをとり、線分ADと線分BEとの交点をFとする。∠BFD=60°のとき、△ABD≡△BCEであることを証明しなさい。

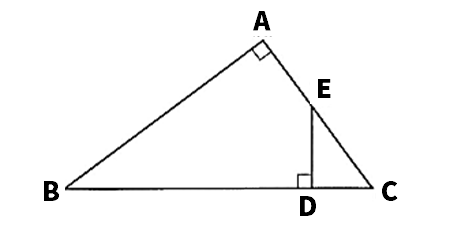
【4】次の図で、△ABCは∠A=90°の直角三角形である。辺BC上にAB=BDとなる点Dをとり、点Dを通る辺BCの垂線と辺ACとの交点をEとする。このとき、AE=DEであることを証明しなさい。

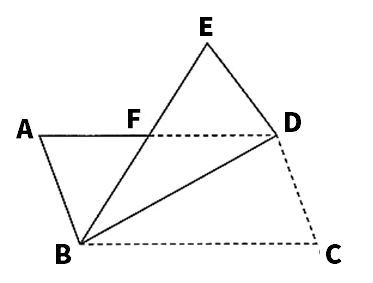
【5】次の図のように、AB<ADである平行四辺形ABCDを、対角線BDを折り目として折り返し、折り返したあとの頂点Cの位置をEとする。辺ADと線分BEとの交点をFとするとき、△ABF≡△EDFであることを証明しなさい。

【6】次の図で、四角形ABCDはAD//BCの台形である。辺CDの中点をEとし、線分AEの延長と辺BCの延長との交点をFとする。点Aと点C、点Dと点Fを結ぶとき、四角形ACFDは平行四辺形になることを証明しなさい。

【解答・解説】図形の合同の証明（中2数学）

【1】
△EBOと△FDOにおいて、
正方形の対角線はそれぞれの中点で交わるから、BO=DO…➀
対頂角は等しいから、∠BOE=∠DOF…➁
平行線の錯角は等しいから、∠EBO=∠FDO…➂
➀➁➂より、1組の辺とその両端の角がそれぞれ等しいから、△EBO≡△FDO

【2】
△ADCと△BDEにおいて、
仮定より、DC=DE…➀
∠ADB=90°、∠ABD=45°より、△ABDは直角二等辺三角形だから、AD=BD…➁
∠ADC=∠BDE…➂
➀➁➂より2組の辺とその間の角がそれぞれ等しいから、△ADC≡△BDE

【3】
△ABDと△BCEにおいて
△ABCは正三角形だから、AB=BC…➀
△ABCは正三角形だから、∠ABD=∠BCE…➁
∠BAD=∠BFD-∠ABF=60°-∠ABF…➂
∠CBE=∠ABD-∠ABF=60°-∠ABF…④
➂➃より、∠BAD=∠CBE…➄
➀➁➄より、1組の辺とその両端の角がそれぞれ等しいから、△ABD≡△BCE

【4】
点Bと点Eを結ぶ。
△ABEと△DBEにおいて、
仮定より、∠BAE=∠BDE=90°…➀
AB=DB…➁
共通な辺だから、BE=BE…➂
➀➁➂より、直角三角形で、斜辺と他の1辺がそれぞれ等しいから、△ABE≡△DBE
よって、AE=DE

【5】
△ABFと△EDFにおいて、
平行四辺形の対辺だから、AB=DC…➀
折り返した辺だから、ED=DC…➁
➀➁より、AB=ED…➂
平行四辺形の対角だから、∠BAF=∠C…④
折り返した角だから、∠DEF=∠C…➄
➃➄より、∠BAF=∠DEF…⑥
対頂角だから、∠AFB=∠EFD…⑦
⑥⑦より、残りの角も等しいから、
∠ABF=∠EDF…⑧
➂⑥⑧より1組の辺とその両端の角がそれぞれ等しいから、△ABF≡△EDF

【6】
△AEDと△FECにおいて、
点Eは辺CDの中点だから、DE=CE…➀
対頂角だから、∠AED=∠FEC…➁
AD//CFだから、∠ADE=∠FCE…➂
➀➁➂より、1組の辺とその両端の角がそれぞれ等しいから、△AED≡△FEC
よって、AD=FC…➃
➃とAD//CFより、1組の対辺が平行でその長さが等しいから、四角形ACFDは平行四辺形になる。

〔別解〕
△AEDと△FECにおいて、
点Eは辺CDの中点だから、DE=CE…➀
対頂角だから、∠AED=∠FEC…➁
AD//CFだから、∠ADE=∠FCE…➂
➀➁➂より、1組の辺とその両端の角がそれぞれ等しいから、△AED≡△FEC
よって、AE=FE…➃
➀と➃より、対角線がそれぞれの中点で交わるから、四角形ACFDは平行四辺形になる。