中1数学の「図形の移動(平行・回転・対称)」についてまとめています。図形の移動に関して、線分、距離など用語についてもふれています。覚えるべきことをまず覚えて学習に入りましょう。それでは、中1数学の「図形の移動(平行・回転・対称)」です。
直線図形
- 線分…まっすぎに限りなくのびている直線といい、その一部のでその両端のあるものです。
2点間の距離…2点A,Bをつなぐ線のうち。もっとも短い線分ABのの長さ。 - 垂直…2直線AB、CDが交わってできる角が直角であるとき。ABとCDは垂直であるといい、AB⊥CDと表します。
- 平行…2直線AB、CDが交わらないとき、ABとCDは平行であるといい、AB//CDと表します。
その他記号
- 角の記号「∠」
- 三角形の記号「△」
図形の移動
図形の形と大きさを変えないで、位置だけを変えることを移動といいます。
平行移動
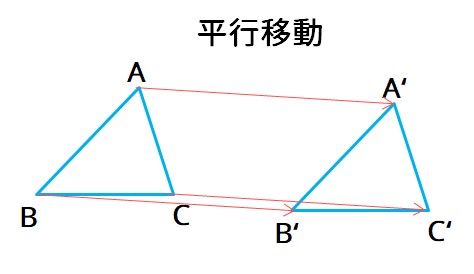
平行移動は、平面上で、図形を一定の方向に、一定の長さだけずらして、その図形を移すことです。平行移動では、対応する点を結んだ線分がそれぞれ平行で、その長さは等しいです。
回転移動
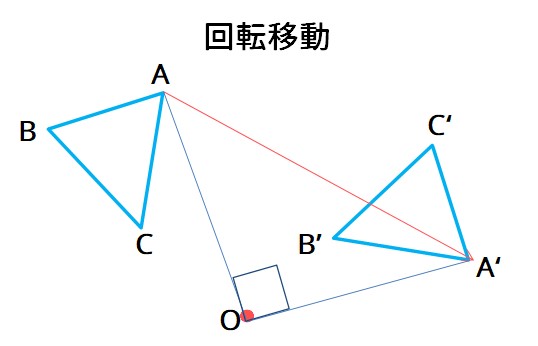
回転移動は、平面上で、図形を1つの点Oを中心として、一定の角度だけをまわして、その図形を移すことです。ちゅうしんとした点Oを開店の中心といいいます。特に、回転移動の中で180°の回転移動を点対称移動といいます。回転移動では、対称する点は、回転の中心から距離が等しく、回転の中心と結んできた角の大きさは、すべて等しいです。
対称移動
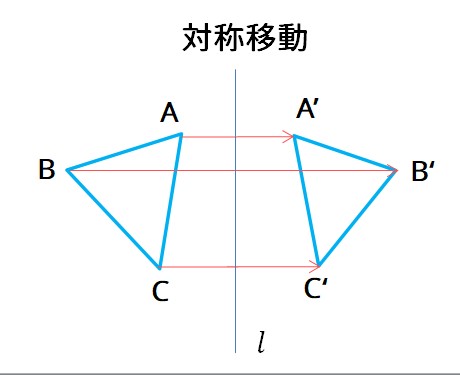
対称移動は、平面上で、図形を1つの直線lを折り目として、折り返して、その図形を移すことです。直線lを大将の軸といいます。
中点・垂直二等分線
線分の両端から距離が等しい線分上の点を、その線分の中点といいます。線分の中点を通り、その線分と垂直に交わる直線をその線分の垂直二等分線といいます。線分ABの垂直二等分線上の点は、線分ABの両端の点A、Bからの距離が等しいです。2点A,Bからの距離が等しい点は、線分ABの垂直二等分線上にあります。
角の二等分線
角の二等分線は、角を2等分する直線のことをいいます。角の二等分線上の点は、角の2辺から等しい距離にあります。角の2辺から等しい距離にある点は、その角の二等分線上にあります。
以上が、中1数学の「図形の移動(平行・回転・対称)」となります。覚えることが多いので、しっかり覚えていきましょう。


コメント