【高校入試対策数学・空間図形】頂点から下ろした垂線の長さを求める練習問題

【高校入試対策数学・空間図形】頂点から下ろした垂線の長さを求める練習問題です。

【問題】頂点から下ろした垂線の長さを求める練習問題

次の図のように、一辺の長さが6ｃｍの立方体ＡＢＣＤ-ＥＦＧＨがある。辺ＢＦ、ＤＨ上の中点をそれぞれＰ、Ｑとする。次の各問いに答えよ。

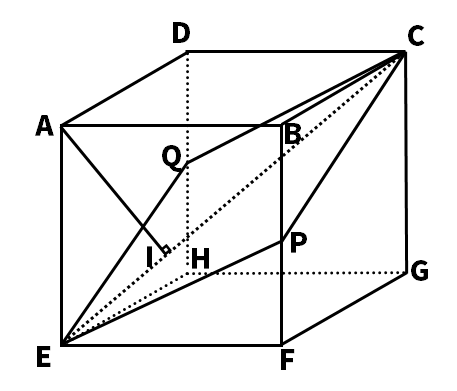
基本問題（1）ＣＰの長さを求めなさい。

基本問題（2）ＣＥの長さを求めなさい。

標準問題（3）平面ＥＰＣＱの面積を求めなさい。

応用問題（4）Ａから平面ＥＰＣＱに垂線ＡＩを引くとＩは線分ＣＥ上にある。四角錘Ａ-ＥＰＣＱの体積を求めなさい。

【解答・解説】頂点から下ろした垂線の長さを求める練習問題

（1）3√5cm
【解説】

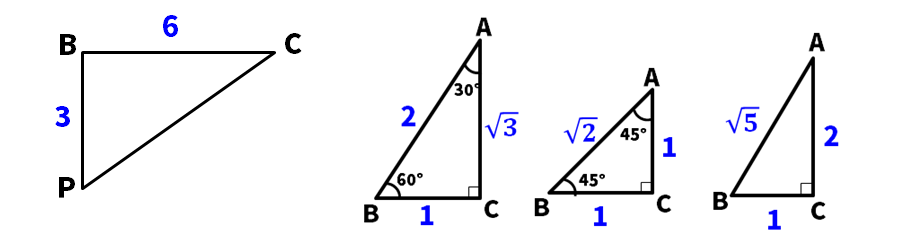
今回求める必要な図を抜き出すと、直角三角形の中でも、1：2：√5の三平方の定理が使える直角三角形が現れます。知らなかった人は、この機会に使えるようにしましょう！

（2）6√3cm
【解説】

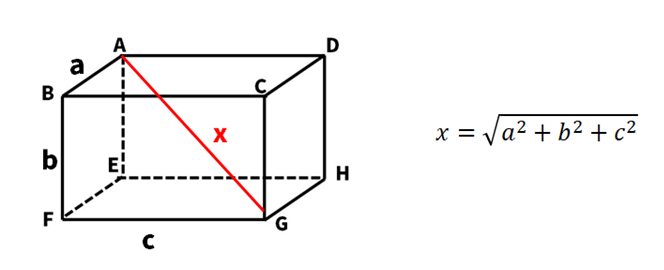
空間の対角線を求める公式＝「（縦の長さ）²＋（横の長さ）²＋（高さの長さ）²」を使うと便利ですね！

（3）18√6cm²
【解説】

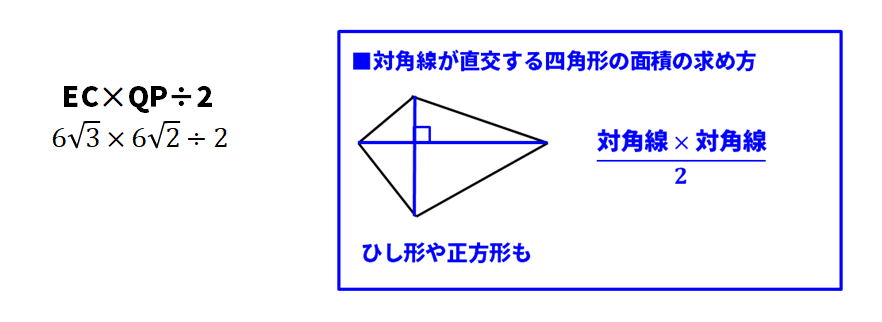
求める四角形は対角線が直交するので、公式にあてはめて解きましょう！対角線が直交する四角形を求める公式＝「（対角線×対角線）÷2」です。知らなかった人は、この機会に使えるようにしましょう！

（4）72cm³
【解説】

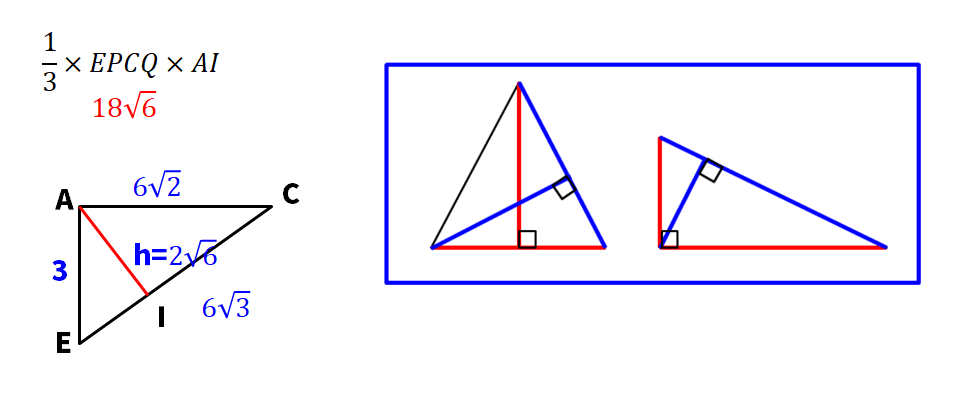
まず、垂線を下ろした長さ（＝AIの長さ）を求めるのが今回の最大のポイントです！図にあるように2方面から同じ面積を求める形で方程式を作って、求めるのがコツです！今回は、求める長さをhとすると、6√3×h＝3×6√2の方程式ができますね。これは、△ＡＥＣの面積を2方面から求めることで成立している方程式となっているわけですね！