相似条件に合うように、相似な組を見つける問題と相似を利用して、線分の長さの練習です。
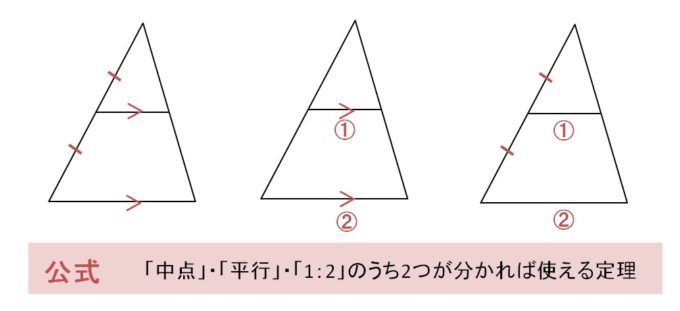
➊3組の辺の比がすべて等しい。
➋2組の辺の比が等しく、その間の角が等しい。
➌2組の角がそれぞれ等しい。
相似な図形の定期テスト対策問題
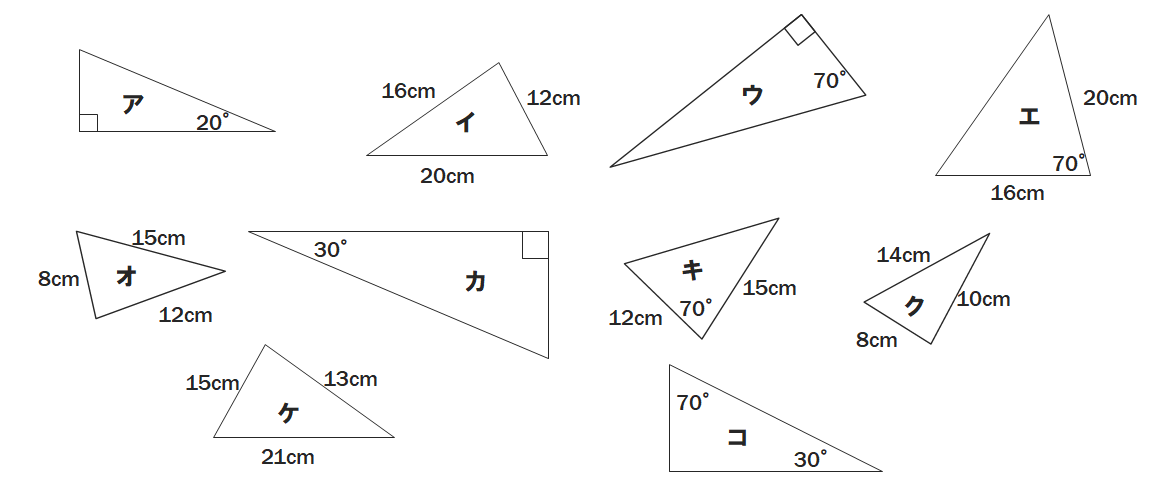
問1 次の図の三角形の中から、相似な三角形の組を選びなさい。またそのときの相似条件も書きなさい。
問2 次の図で、DE//BCのとき、次の問いに答えなさい。
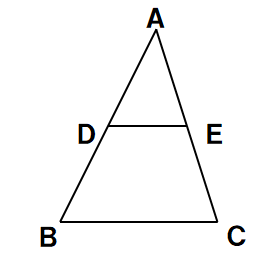
(1)AD=8、AB=12、DE=6であるときのBCの値を求めよ。
(2)AD=5、DE=3、BC=9であるときのDBの値を求めよ。
(3)AD=6、AB=9、AC=12であるときのAEの値を求めよ。
問3 次の図で、DE//BCのとき、次の問いに答えなさい。
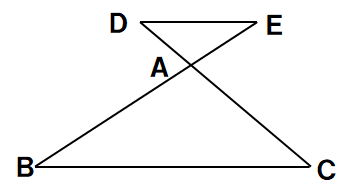
(1)DE=6、BC=9、DA=4であるときのACの値を求めよ。
(2)DE=9、BC=15、AE=6であるときのABの値を求めよ。
問4 次の図で、a//b//cのとき、xの値を求めなさい。

問5 次の図で、a//b//cのとき、xの値を求めなさい。
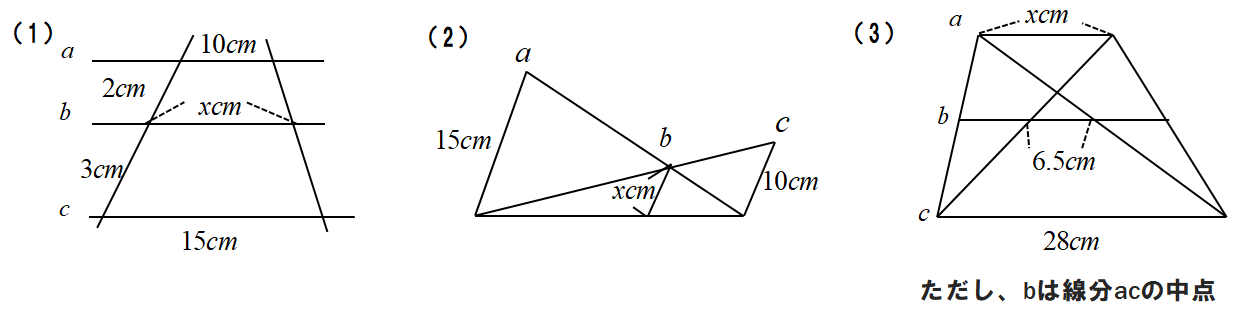
問6 次の△ABCで、D,Eは辺ABを3等分する点、Fは辺BCの中点である。EF=14cmのとき、次の問いに答えなさい。
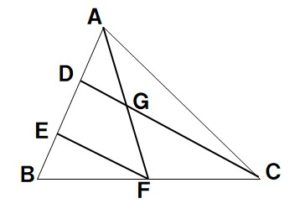
(1)DGの長さを求めなさい。
(2)GCの長さを求めなさい。
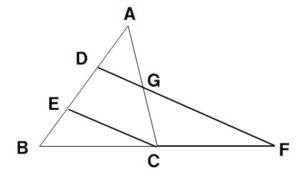
問7 次の△ABCで、D,Eは辺ABを3等分する点、BCの延長と、点Dを通りECに平行な直線との交点をFとする。ACとDFとの交点をGとし、GF=7cmのとき、DGの長さを求めよ。
相似な図形の定期テスト対策問題解答
問1
アとウ 2組の角がそれぞれ等しい
エとキ 2組の辺の比とその間の角がそれぞれ等しい
問2
(1)9
(2)10
(3)8
問3
(1)6
(2)10
問4
(1)8
(2)9/2
(3)12
問5
(1)12
(2)6
(3)15
問6
(1)7cm
(2)21cm
問7
(3)7/3cm
DG=xとすると、EC=2x
2×EC=EF
2×2x=x+7
4x=x+7
3x=7
x=7/3


コメント