【中3数学】二次関数の定期テスト対策問題

【中3数学】二次関数の定期テスト対策問題です。定期テストレベルの問題で編集されています。

基本の確認はこちらから。
基本問題 【中3数学】テストで頻出のニ次関数の基本総合問題

【対策問題】二次関数

【1】次の問いに答えなさい。
（1）yはxの2乗に比例し、x=3のときy=18である。yをxの式で表しなさい。

（2）yはxの2乗に比例し、x=2のときy=-12である。x=-3のときのyの値を求めなさい。

（3）yはxの2乗に比例し、x=3のときy=6である。y=12となるときのxの値をすべて求めなさい。

【2】次の問いに答えなさい。
（1）関数y=2x²について、xの値が1から3まで増加するときの変化の割合を求めなさい。

（2）関数y=ax²について、xの値が2から6まで増加するときの変化の割合が-4であった。このとき aの値を求めなさい。

（3）関数y=3x²について、xの変域が−2≦x≦1のときのyの変域を求めなさい。

（4）関数y=ax²について、xの変域が-1≦x≦4のときのyの変域が-4≦y≦0であった。このとき、aの値を求めなさい。

【3】次の図のように、関数y=1/2x²…➀のグラフと直線➁が2点A、Bで交わっており、点Aのx座標は-2、点Bのy座標は8である。これについて、次の問いに答えなさい。ただし、点Bのx座標は正であるものとする。

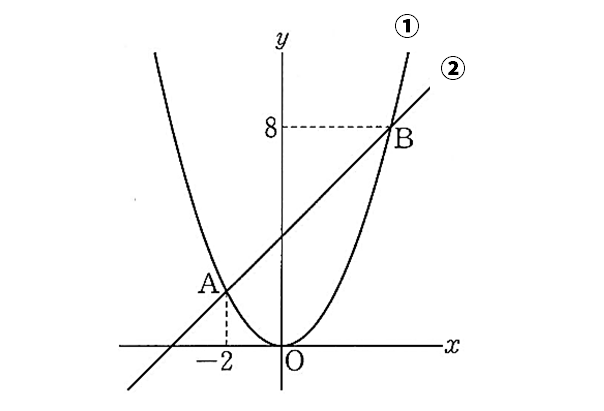
（1）点A、Bの座標をそれぞれ求めなさい。
（2）直線➁の式を求めなさい。

【4】図のように、ｙ軸上の点P（0,16）を通って、x軸と平行な直線と関数y=x²との交点のうち、ｘ座標が正のものをQとする。このとき、次の問いに答えよ。

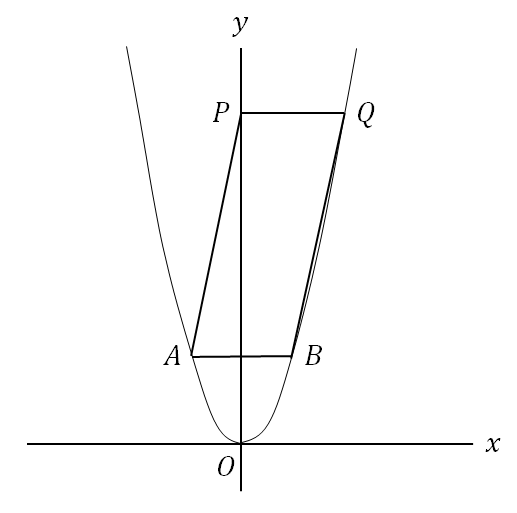
（1）点Qの座標を求めよ。
（2）放物上に2点A,Bをとり、四角形PABQを平行四辺形となるようにつくる。原点Oを通り、この平行四辺形の面積を2等分する直線の式を求めよ。

【5】次の問いに答えなさい。
（1）関数y=2×2のグラフについて、xの変域が以下のときyの変域を求めよ。
➀2≦x≦4
➁-2≦x≦4
➂-4≦x≦2

（2）関数y=ax2のxの変域を-2≦x≦1のときのyの変域がb≦y≦8になる。このとき、a、bの値を求めよ。

（3）関数y=3×2で、xの変域が-2≦x≦aのとき、yの変域がb≦y≦27となった。このとき、aの値とbの値を求めよ。

【6】次の問いに答えなさい。
（1）関数y=2x²について、xの値が2から4まで増加するときの変化の割合を求めよ。

（2）関数y=－2x²について、xの値が1から4だけ増加するときの変化の割合を求めよ。

（3）関数y=ax²について、xの値が1から3まで増加するときの変化の割合が8であった。このときaの値を求めなさい。

（4）関数y=ax²について、xの値が-1から4まで変化するときの変化の割合が、y=-3x+2の割合と等しいとき，aの値を求めなさい。

（5）高いところから物を自然に落とすとき、落ち始めてからx秒後までに落ちる距離をymとすると、y=5x²という関係がある。落ち始めてから4秒後までの平均の速さを求めよ。

【解答・解説】二次関数

【1】
（1）y=2x²
（2）y=-27
（3）x=±3√2

【2】
（1）8
（ポイント）関数y=ax2の変化の割合は、1次関数のように一定ではない(aとは一致しない)ので、注意しよう。

（2）a=-1/2

（3）0≦y≦12
（ポイント）変域について考えるときは、グラフの大まかな形をかいて、最大の値と最小の値を調べよう。

（4）a=-1/4

【3】
（1）A（-2，2）　B（4，8）
（2）y=x+4

【4】
（1）（4，16）
（2）y=10x
（ポイント）平行四辺形の面積を二等分する直線は必ず対角線の交点を通る。

【5】
（1）➀8≦y≦32 　➁0≦y≦32　➂0≦y≦32
（2）a=2 b=0
（3）a=3 b=0

【6】

（1）12
（2）-10
（3）a=-2
（4)  a=-1
（5）20m/秒