【中3数学】二次方程式文章題の練習問題

【中3数学】二次方程式文章題の練習問題です。

【練習問題】二次方程式文章題

【1】連続した3つの自然数がある。最も小さい数と真ん中の数の和の4倍は、最も大きい数の2乗より12小さくなる。最も小さい自然数をxとして2次方程式をつくり、それを解いて、連続した3つの自然数を求めなさい。

【2】1辺の長さがxcmの正方形がある。この正方形の縦の辺を2cm、横の辺を4cmのばしてできた長方形の面積は、もとの正方形の面積の3倍となった。このとき、xの値を求めなさい。

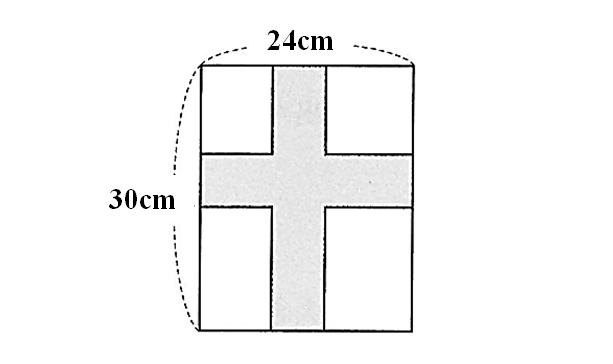
【3】縦30cm、横24cmの長方形の白い画用紙に、次の図のように縦と横に同じ幅で色をぬると、白い部分の面積がもとの画用紙の面積の3/5（5分の3）倍になった。このとき、色をぬった部分の幅を求めなさい。ただし、色をぬった部分の幅をxcmとして方程式をつくり、答えを求めるまでの過程も書きなさい。

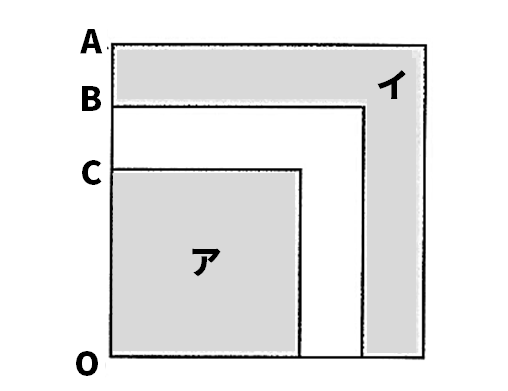
【4】次の図のように、線分OAを1辺とする正方形がある。辺OA上にAB=1cm、AC=2cmとなるように2点B、Cをとり、OAを1辺とする正方形と同じ側に、2つの線分OB、OCを1辺とする正方形をそれぞれつくる。アの部分の面積とイの部分の面積が等しいとき、OCの長さを求めなさい。ただし、用いる文字が何を表すかを示して方程式をつくり、それを解く過程も書きなさい。

【5】次の問いに答えなさい。
（1）連続した3つの自然数がある。その最小の数の平方は、残りの2数の和に等しくなります。最小の数をｘとして、式をつくり連続する3つの自然数を求めなさい。ただし、途中の式も書きなさい。

（2）大小3つの数がある。大きい数は小さい数より4大きく、この2つの数の積は、この2つの数の和を5倍した数より４小さい。小さい方の数をｘとして、大きい数と小さい数をそれぞれ求めなさい。途中式も書け。

【解答・解説】二次方程式文章題

【1】真ん中の数はx+1、最も大きい数はx+2だから
{x+(x+1)}×4=(x+2)2-12
(x+2)(x-6)=0
x=-2,6
xは自然数だから、x=6。
よって、求める3つの自然数は6、7、8

＜解答＞6、7、8

【2】長方形の縦の長さは(x+2)cm、横の長さは(x+4)cmだから
長方形の面積について、(x+2)(x+4)=3x
これを解くと
(x+1)(x-4)=0
x=-1,4
x>0だから
x=4

＜解答＞4cm

【3】色をぬった部分の幅をxcmとする。
色をぬった部分を端によせると、白い部分は縦が(30-x)cm、横が (24-x) cmの長方形になるから
白い部分の面積について
(30-x) (24-x)=30×24×3/5（5分の3）
これを解くと、
(x-6)(x-48)=0
0<x<24 だから、x=6

＜解答＞6cm

【4】OCの長さをxcmとすると、
アの部分の面積はx²(cm²)
また、BCの長さは、2-1=1(cm)だから、
イの部分の面積は、
(x+2)²-(x+1)²=2x+3(cm²)
アとイの面積が等しいからx²=2x+3
これを解くと
(x+1)(x-3)=0
x=-1,3
x>0だからx=3

＜解答＞3cm

【5】
（1）
真ん中の整数をnとすると、連続した3つの自然数は、n-1,n,n+1と表せる。
(n-1)2=n+(n+1)
n2-2n+1=2n+1
n2-4n=0
n(n-4)=0
n=0,4
n＞0より、n=0は問題に合わない。
よって、3,4,5

（2）
小さい数をnとすると、大きい数はn+4と表せる。
n(n+4)= 5{n+(n+4)}-4
n2-6n-16=0
(n+2)(n-8)=0
n=-2,8

これは、問題に合う。
よって、
小さい数が-2のとき、大きい数は2
小さい数が8のとき、大きい数は12となる。