物体の運動のようすを観察するために、力学台車を使った実験があります。今回はそのポイントを学習しましょう。
台車の運動と速さ
力学台車を、下の図のようなコースで運動させると、速さは下のグラフのように変化します。
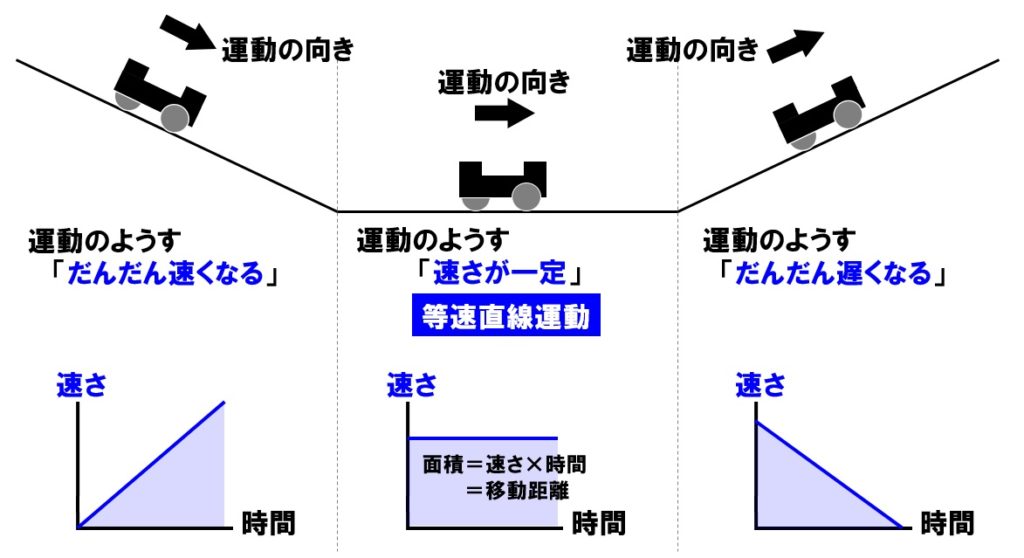
斜面を下る運動の速さの変化
台車の速さは、だんだん大きく（速く）なります。このとき、斜面の傾きが一定なので、一定の割合で速さが大きく（速く）なることも重要です。つまり比例します。
摩擦のない水平面上を運動するときの速さの変化
台車の速さは一定になります。この速さが変化しない運動を等速直線運動といいます。
斜面を上る運動の速さの変化
台車の速さは、だんだん小さく（遅く）なります。このとき、斜面の傾きが一定なので、一定の割合で速さが遅くなります。
次は物体の運動について見ていきましょう。
台車の運動と力
台車の速さの変化の仕方が、それぞれの運動で異なるのは、台車にはたらく力の向きが異なるからです。下の力の向きをしっかりと確認しましょう。
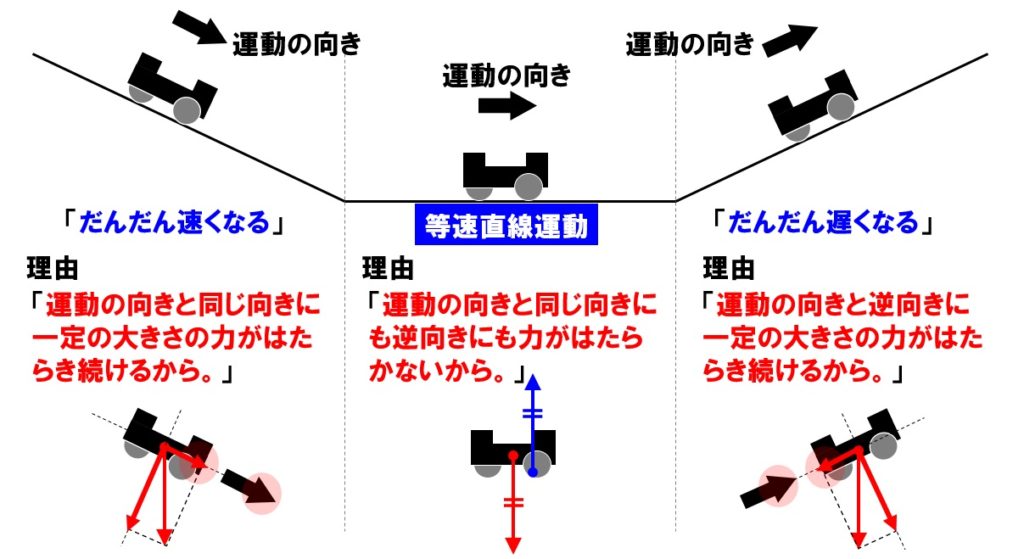
斜面を下る運動の力
台車がだんだん速くなる理由は、台車の運動の向きと同じ向きに力がはたらくからです。また、一定の割合で速さが速くなるのは、台車の運動の向きと同じ向きに、一定の大きさの力がはたらき続けるからです。
摩擦のない水平面上を運動するときの力
台車の速さが一定なるのは、台車の運動の向きと同じ向きにも、逆向きにも力がはたらいていないからです。このとき台車にはたらいている力は、重力と垂直抗力だけで、この2つの力はつり合いの関係にあります。つり合って、打ち消し合って、合力が０になっています。
斜面を上る運動の力
台車の速さがだんだん遅くなる理由は、台車の運動の向きと逆向きに力がはたらくからです。また、一定の割合で速さが遅くなるのは、台車の運動の向きと逆向きに、一定の大きさの力がはたらき続けるからです。
台車の運動とグラフ
台車の運動では、時間経過と速さや移動距離、台車の運動の向きの力などが選択問題として出題されます。正しいグラフをかけるようになっておきましょう。
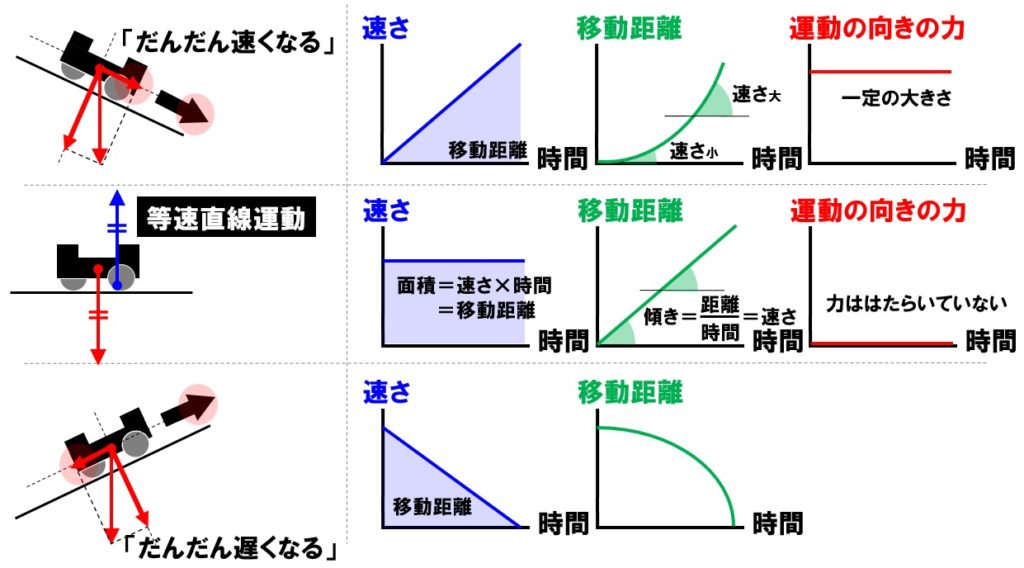
斜面を下る運動のグラフ
- 速さ…一定の割合でだんだん速くなるので比例のグラフ
- 移動距離…傾きが速さを表すので、傾きがだんだん大きくなるグラフ
- 運動の向きの力…斜面の傾きが一定なので、一定の大きさのグラフ
摩擦のない水平面上を運動するときのグラフ
- 速さ…等速直線運動をするので、一定の大きさのグラフ
- 移動距離…傾き（速さ）が変化しない比例のグラフ
- 運動の向きの力…運動の向きに力ははたらいていない
斜面を上る運動のグラフ
- 速さ…一定の割合でだんだん遅くなるグラフ
- 移動距離…傾きが速さを表すので、傾きがだんだん小さくなるグラフ
- 運動の向きの力…運動の向きと逆向きに一定の力がはたらくグラフ
【対策問題】台車の運動と記録タイマー
下の図のような装置を用いて、斜面を下る台車の運動のようすを調べる実験をした。あとの各問いに答えよ。
【実験】
図のように、なめらかで十分に長い斜面上に台車をのせて、静かに手をはなし、1秒間に50回打点する記録タイマーで台車の運動のようすを記録した。下の図の記録テープはこのときのようすを表したものである。
（1）記録タイマーが、図のＡの打点を記録してからＢを打点するまでにかかって時間は何秒か。
（2）台車が図のBC間を運動したときの平均の速さは何cm/sか。
（3）図の記録テープの最初の方を使わない理由を、簡潔に答えよ。
（4）記録タイマーが、図のAを打点してから、0.4秒間に進んだ距離は何cmか。
（5）斜面上の台車に運動の向きにはたらいている力について、正しく述べているものは次のうちどれか。
ア しだいに大きくなるようにはたらいている。
イ しだいに小さくなるようにはたらいている。
ウ 常に一定の大きさではたらいている。
エ 運動の向きに力ははたらいていない。
（6）この台車が斜面を下り始めたときからの時間と、台車の移動距離との関係をグラフに表すと、どのようになると考えられるか。上のア～エの中から選び、記号で答えよ。
【解答・解説】台車の運動と記録タイマー
（1）0.1秒
1秒間に50回打点する記録タイマーの場合、1打点記録するのに1/50秒かかります。図のAB間の打点は5打点になっているので、かかった時間は1/50秒×5打点＝0.1秒になります。
（2）60cm/s
BC間の距離は、9.6－3.6＝6.0cm
BC間を運動するのにかかった時間は、5打点なので0.1秒になります。したがって、このときの台車の平均の速さは、
6.0cm÷0.1s＝60cm/s
となります。
（3）打点が重なっていてわかりにくいから。
記録テープの最初の方の打点は重なっており、1打点間がわかりにくくなっています。
（4）28.8cm
0.1秒ごとの台車の進んだ距離は、
AB間…3.6cm
BC間…9.6－3.6＝6.0cm
CD間…18.0－9.6＝8.4cm
つまり、0.1秒間に進んだ距離が、0.1秒ごとに2.4cmずつ大きくなっていることがわかります。したがって、D点が打点された後の0.1秒間で、
8.4＋2.4＝10.8cm
の長さになることがわかります。なので0.4秒間で台車は、
18.0＋10.8＝28.8cm
進むことがわかります。
（5）ウ
台車がのっている斜面は、一定の傾きになっていますので、台車の重力の斜面に平行な分力は、台車が斜面を運動している間一定の大きさになります。
（6）ア
斜面を下る台車の運動では、時間に比例して速さが大きくなるので、時間が2倍、3倍になると、速さは2倍、3倍になり、時間の2乗に比例する移動距離は、4倍、9倍となります。
コメント