天体の中で計算が必要な日周運動と年周運動に関する問題に挑戦します。
時間や方角の計算問題
天体では、日周運動と年周運動による天体が見える方角や時間の計算問題が出題されます。この計算問題が解けるように練習していきましょう。
計算問題に入る前に、日周運動と年周運動について復習しておきましょう。日周運動は、地球の自転によって起こる見かけの運動でした。地球がその場でコマのように1日に1回転することで、動いていない星座や太陽が動いていくように見えます。
年周運動は、地球の公転によって起こる見かけの運動でした。地球が太陽の周りを1年かけて1周することで、同じ時刻に見える星座や星の位置が変化しました。下に表でまとめています。
| 方角 | 角度 | 原因 | |
| 日周運動 | 東から西 | 1時間で15° | 地球の自転 |
| 年周運動 | 東から西 | 1か月で30° | 地球の公転 |
北の空では、北極星を中心に反時計回りに動いていくように見えましたね。
日周運動の計算問題
まずは日周運動だけの問題に挑戦しましょう。ポイントは時刻の変化です。1時間で15°東から西、北の空なら反時計回りに星座や星が動くのがポイントです。
問題1
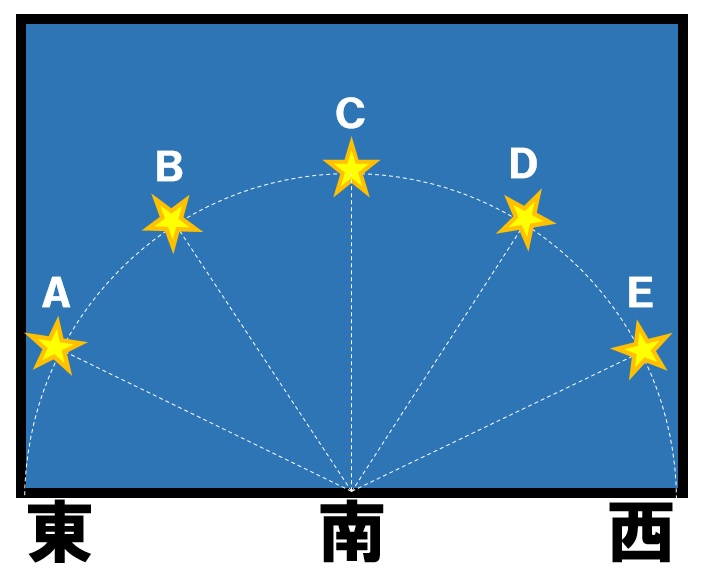
まず確認することは方角です。この問題では南の空を観察しているので、星は東から西に動いていくように見えます。
次に確認するこは時刻です。時刻を確認すると、最初は午後7時に観察し、次に午後11時に観察しています。12時制で考えるとわかりにくいので24時制に直して計算していきましょう。
- 午後7時→19時
- 午後11時→23時
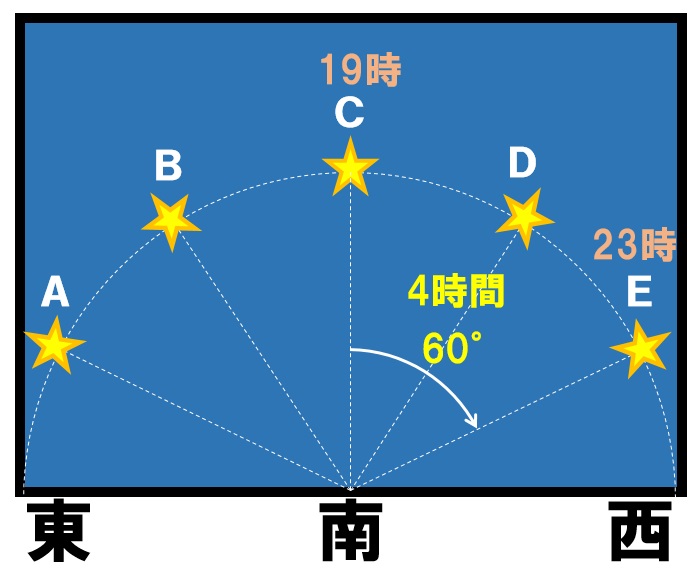
経過した時間は、23時-19時=4時間
4時間経過すると日周運動で、15°×4時間=60°
星は東から西に60°動いて見えます。したがって答えはEです。
問題2
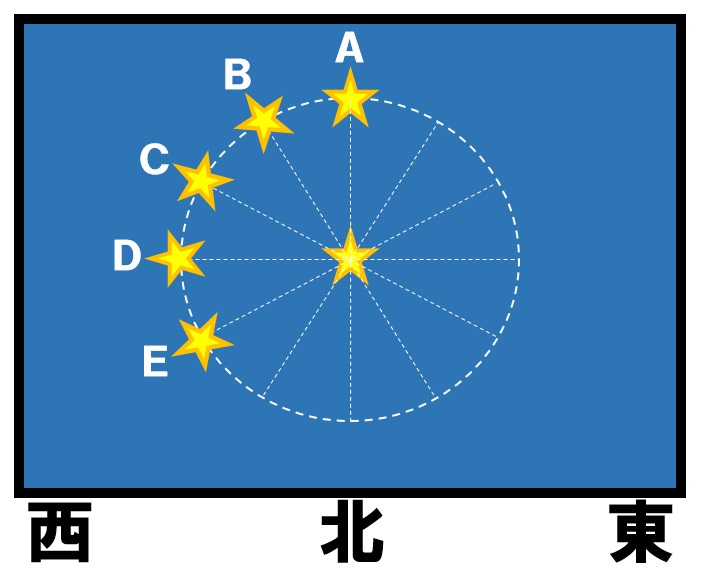
まずは、方角を確認します。北の空のの星の動きですので、北極星を中心に反時計回りに星が動いていくように見えます。
次に時刻を確認します。午後10時、24時制では22時に星をBの位置に観察しています。
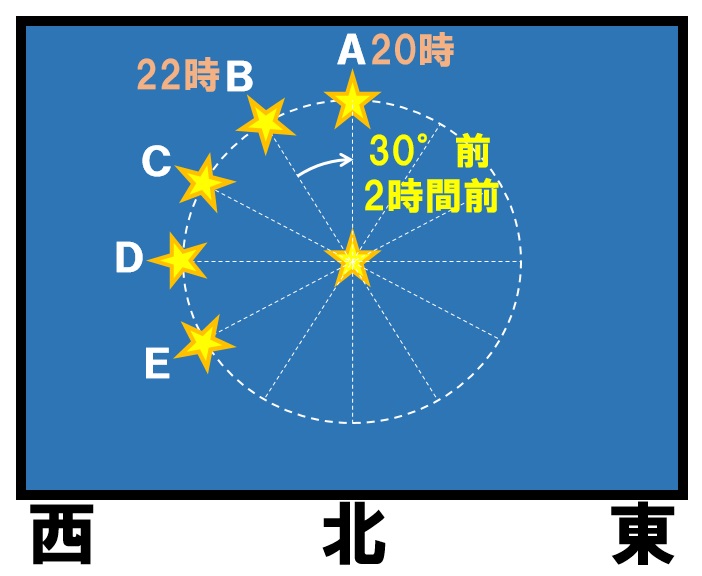
この星がAの位置に見えた時刻を求めればいいので、AはBと比べ何度先にあるのか、何度前にあるのかを考えます。図を確認すると30°前にあることがわかりますので、
-30°÷15°=-2時間
つまり2時間前に観察したことになります。
22時-2時間=20時
したがって答えは、午後8時になります。
年周運動の計算問題
次は年周運動に関する計算問題です。年周運動が絡む問題では日付が変化します。1か月経てば星座や星は30°東から西、北の空なら反時計回りに動いていくように見えるのがポイントです。
問題1

まず方角を確認します。南の空の星の動きですから1時間で15°、1か月で30°東から西に星が動いていきます。
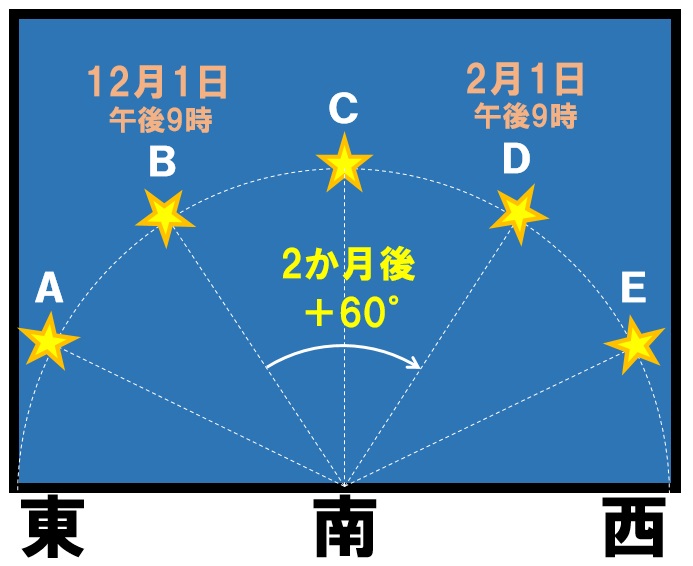
時刻は変化していませんが、12月1日から2月1日に日付が変わっています。つまり2月後に観察を行っていますので、星は東から西に次の角度移動しています。
30°×2か月=60°
60°東から西に星が移動しているので、星はB→Dに移動しています。
したがって答えはDとなります。
問題2

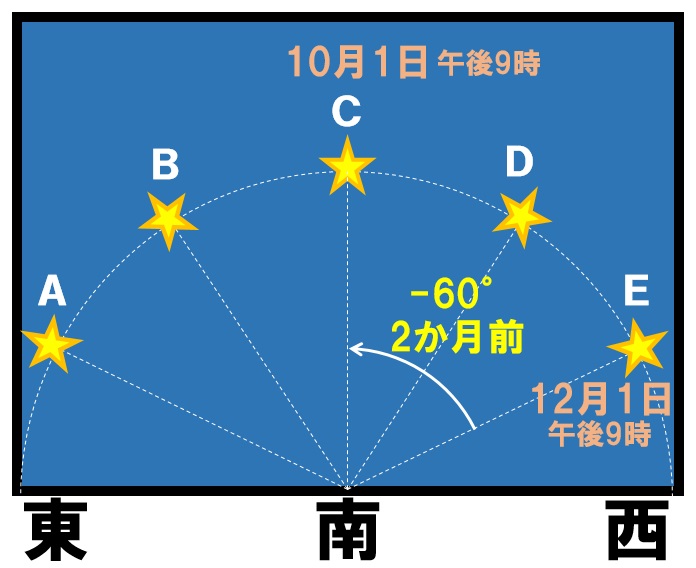
まず方角を確認します。南の空の星の動きですので東から西に星が運動します。
時刻は変わりませんが、日付は変わっているはずです。Eの位置に見えた星が60°前のCの位置(南中)に見えるのは2か月前の10月1日になります。
日周運動と年周運動の混ざった問題
日周運動と年周運動の両方が混じった問題では、時刻も日付も変わります。1時間で15°と1か月で30°の両方を使って計算していきます。
問題

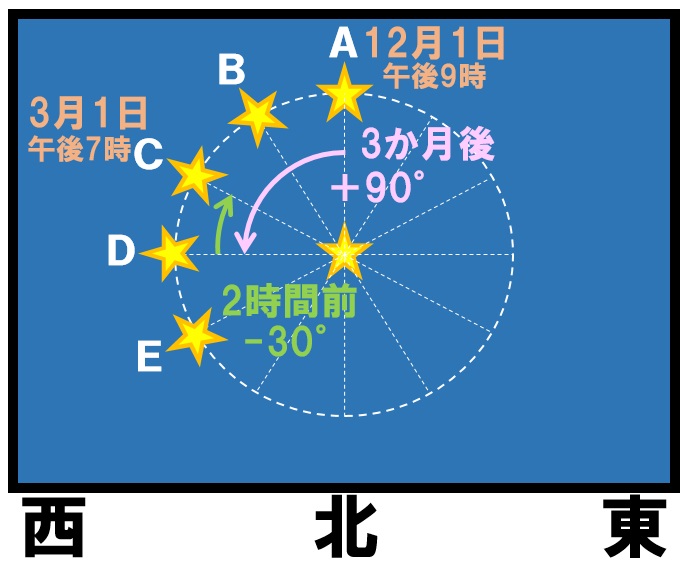
北の空の星の動きですので、反時計回りに星が動いて見えます。時刻と日付が変わっているので、図に書き込んだり、表にまとめるなどして計算していきます。
時刻と日付の変化
- 午後9時→午後7時
2時間前
2時間前なので15°×2時間=30°前に見える - 12月1日→3月1日
3か月後
3か月後なので30°×3か月=90°先に見える
ということは-30°+90°=60°先に見えることになります。
したがって答えはCとなります。


コメント