【中3理科】力学的エネルギーの定期テスト対策問題

位置エネルギーと運動エネルギーの和である力学的エネルギーについて演習を行います。まずは、確認問題で基礎知識を確認しましょう。

力学的エネルギーの保存の確認問題

1. エネルギーとは、他の物体に何をする能力のことか。
2. 位置エネルギーは、物体の何と何に比例して大きくなるか。
3. 運動エネルギーは、物体の質量に比例し、何の2乗に比例するか。
4. 物体の質量を3倍、速さを2倍にすると運動エネルギーは何倍になるか。
5. 位置エネルギーと運動エネルギーの和を何というか。
6. 空気の抵抗や摩擦がない場合、５はどうなるか。
7. ６のことを何というか。
8. 10mの高さにある物体が、斜面を下って6mの高さA点を通過し、最下点の0m地点を通過した。最下点を通過するときの運動エネルギーはA点を通過するときの運動エネルギーの何倍か。

解答

1. 仕事
2. 高さと質量
3. 速さ
4. 3×2²＝12倍
5. 力学的エネルギー
6. 一定になる。
7. 力学的エネルギーの保存（力学的エネルギー保存の法則）
8. 2.5倍

【練習問題❶】位置エネルギーと木片の移動距離

下の図のような装置で、質量が10g、20g、30gの3つの小球を、高さを変えて転がして木片に衝突させ、小球と木片が一体となって動く距離をはかった。その結果がグラフのようになった。次の各問いに答えよ。

1. 10gの小球の結果は、グラフのA～Cのうちのどれか。記号で答えよ。
2. 10gの小球を6cmの高さから転がしたときの木片の移動距離を、30gの小球で動かすためには何cmの高さから転がせばよいか。
3. 小球の持つエネルギーの大きさは、小球の高さおよび質量と、それぞれどのような関係があるか。
4. 50gの小球を8cmの高さから転がすと、木片の移動距離は何cmになるか。

【解答・解説❶】位置エネルギーと木片の移動距離

1. C
   小球の持つ位置エネルギーは質量に比例して大きくなるので、小球の質量が大きければ大きいほど、木片の移動距離も大きくなる。したがって、Cが10g、Bが20g、Aが30gだとわかる。
2. 2cm
   グラフを見れば、10g（C）を6cmの高さから転がすと、木片の移動距離は15cmだとわかる。30g（A）の小球を転がして、木片を15cm動かすためには、小球を2cmの高さから転がせばよいとわかる。
3. 高さ：比例する　　質量：比例する
   位置エネルギーは高さと質量に比例します。
4. 100cm
   10g（C）の小球を4cmの高さから転がすと、木片は10cm移動しているので、50gの小球を8cmの高さから転がすと、質量が5倍、高さが2倍で、10g（C）の小球を4cmの高さから転がした場合の10倍の移動距離になります。
   10cm×5×2＝100

【練習問題❷】力学的エネルギーの保存

図１は、ふりこの運動のようすを記録したもので、図２はこのときのおもりの持つ位置エネルギーの変化のようすをグラフに表したものである。これについて、次の各問いに答えなさい。ただし、ふりこはＡから振り下ろしたものとし、空気の抵抗や摩擦は考えないものとする。

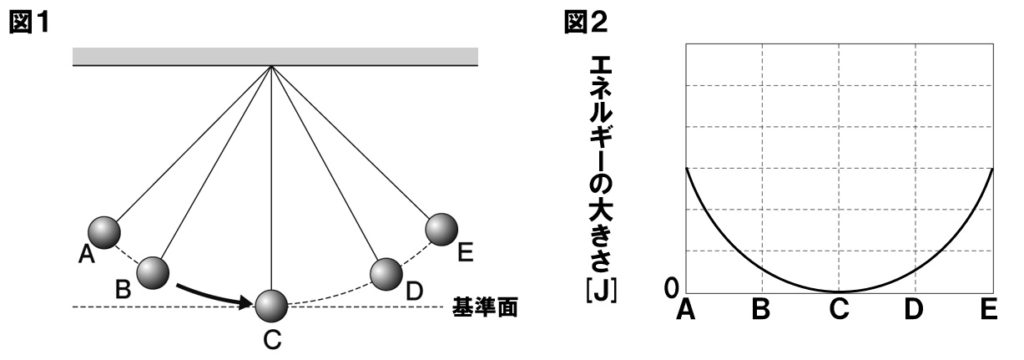
（1）図１のＡ～Ｅの中で、おもりの速さが最大になるのはどれか。すべて選び記号で答えなさい。

（2）図１のＡ～Ｅの中で、おもりの速さが最小になるのはどれか。すべて選び記号で答えなさい。

（3）図１のA～Eの中で、おもりの持つ運動エネルギーが2番目に大きいのはどれか。すべて選び、記号で答えなさい。

（4）おもりが図１のＥ点に達したとき、ふりこの糸を切ると、おもりはその後どのように運動するか。次のア～エから選び、記号で答えよ。
ア　右斜め上に飛び出す。
イ　真横に飛び出す。
ウ　自由落下運動をする。
エ　その場で静止する。

（5）図２のグラフは、おもりがＡ～Ｅまで運動したときの位置エネルギーの変化を表したものである。おもりがＡ～Ｅまで運動したときの運動エネルギーの変化のようすを、図２のグラフに表せ。

（6）位置エネルギーと運動エネルギーの和を力学的エネルギーという。ふりこがＡ～Ｅまで運動するときの、力学的エネルギーの変化をグラフに表すとどうなるか。図２のグラフに表せ。

（7）空気の抵抗や摩擦がない場合、力学的エネルギーは一定に保たれる。このことを何というか。

（8）図１のＡの基準面からの高さを30cm、Ｂの基準面からの高さを10cm、Ｃの基準面からの高さを0cmとすると、Ｃでの運動エネルギーはＢでの運動エネルギーの何倍になるか。

【解答・解説❷】力学的エネルギーの保存

（1）Ｃ

おもりの速さが最大になるのは、おもりの位置エネルギーが全て運動エネルギーに移り変わる最下点になります。

（2）Ａ、Ｅ

おもりの速さが最小になるのは、おもりの位置エネルギーが最大になり、運動エネルギーが最小になる点です。おもりの高さが一番高いところがこれにあたります。

（3）B、D

運動エネルギーは、おもりの速さが速いほど大きくなります。おもりがもっとも速いのは、最下点のCを通過するときで、次に速いのは、BとDを通過するときです。

（4）ウ

おもりが最高点に達したとき、おもりの速さが０になります。ここで、ひもを切ると、おもりは真下に自由落下運動をします。

（5）運動エネルギーのグラフは、位置エネルギーのグラフの正反対のかたちになります。

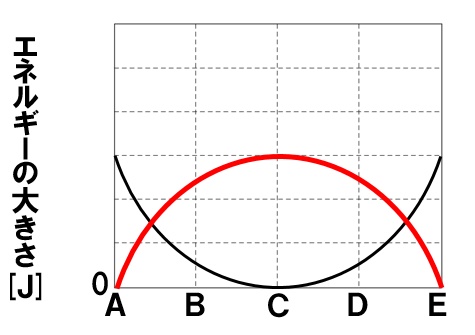
（6）空気の抵抗や摩擦がない場合、位置エネルギーと運動エネルギーの和である力学的エネルギーは一定に保たれます。

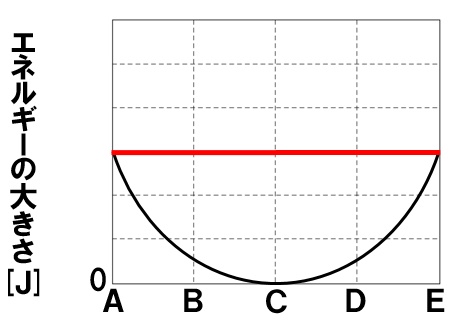
（7）力学的エネルギーの保存（力学的エネルギー保存の法則）

空気の抵抗や摩擦がない場合、位置エネルギーと運動エネルギーの和である力学的エネルギーは一定に保たれることを力学的エネルギーの保存といいます。

（8）1.5倍

Ａでの位置エネルギーを30とすると、運動エネルギーは0、その和である力学的エネルギーは30になります。Ｂでの位置エネルギーは10、力学的エネルギーは保存されるので30、したがって運動エネルギーは、30－10＝20。Ｃでの位置エネルギーは0、力学的エネルギーは保存されて30なので、運動エネルギーは、30－0＝30となります。Ｃでの運動エネルギーはＢでの運動エネルギーの、30÷20＝1.5倍になるとわかります。