中3理科。仕事の学習が終わったら、次はエネルギーの学習になります。まずは、エネルギーとは何なのかを学習し、位置エネルギーと運動エネルギーの和である力学的エネルギーを学習します。空気の抵抗や摩擦がはたらかない場合、力学的エネルギーが保存される計算問題にも挑戦しましょう。
エネルギーとは
エネルギーとは、他の物体に対して仕事をする能力になります。簡単にいうと、エネルギーを持っていると、他の物体にダメージを与えることができるということです。
例えば、運動している車を考えましょう。この車にぶつかることで、人はダメージを受けます。車によって力を受けた向きに移動させられるはずです。ということは、動いている車はエネルギーを持っていることになります。
いろいろなエネルギー
エネルギーには様々なものがありあす。次のエネルギーはよく出てくるので覚えておきましょう。
- 位置エネルギー…基準面より高いところにある物体が持つエネルギー。
- 運動エネルギー…運動している物体がっ持つエネルギー。
- 電気エネルギー…電流が流れている物体や電圧をもっている物体がもつエネルギー。
- 熱エネルギー…熱を持つ物体がもつエネルギー。
- 光エネルギー…光を放つ物体が持つエネルギー。
- 音エネルギー…音を放つ物体が持つエネルギー。
- 化学エネルギー…化学変化を起こすことができる物体が持つエネルギー。
このうち、位置エネルギーと運動エネルギーの和を、力学的エネルギーといいます。
位置エネルギー
位置エネルギーとは、基準面よりも高い位置にある物体が持つエネルギーです。高い場所にある物体は、落下することで他の物体にダメージを与えることができます。鉄球が手元にあっても怖くはありませんが、自分の頭上にあれば恐怖を感じますよね。これは鉄球が高い位置にあり、エネルギーを持っているためです。
では、どのような物体がより大きい位置エネルギーを持っているのでしょうか。どんな物体が頭の上に落ちてきたら怖いか考えましょう。どんな物体が怖いかといえば、より高い場所にある物体で、質量が大きい物体ではないでしょうか。重ければ重いほど、高い場所にあればあるほど頭上に落ちたときのダメージは大きくなるはずです。つまり、位置エネルギーは、物体の高さと質量に比例して大きくなるのです。
❷高さが高いほど大きくなる。（高さに比例する）
❸質量が大きいほど大きくなる。（質量に比例する）
位置エネルギーの確認問題
2mの高さから質量5㎏の物体を床の釘に落下させた場合、釘が1cm床にめり込んだ。次の場合、釘は何cm床にめり込むか。
（1）2mの高さから質量10㎏の物体を床の釘に落下させたとき。
（2）6mの高さから質量5㎏の物体を床の釘に落下させたとき。
（3）4mの高さから質量10㎏の物体を床の釘に落下させたとき。
解答
（1）2cm
質量が2倍になっているので、位置エネルギーも2倍になります。
（2）3cm
高さが3倍になっているので、位置エネルギーも3倍になります。
（3）4cm
質量が2倍、高さが2倍になっているので、位置エネルギーは2倍×2倍＝4倍になります。
位置エネルギーの計算方法
位置エネルギーは計算によっても求めることができます。基準面にある物体は位置エネルギーを持っていません。この物体に重力に逆らって仕事をしてあげると、その分物体は位置エネルギーを持つことになります。仕事は、力の大きさ［N］×移動距離［m］で求めることができます。したがって、位置エネルギーは次の計算式で求めることができます。
位置エネルギー［Ｊ］＝物体の重さ［Ｎ］×高さ［ｍ］
運動エネルギー
運動エネルギーとは、運動している物体が持つエネルギーです。動いてる物体にぶつかると痛いですよね。動いている物体があなたにダメージを与えているからです。
では、どのような物体がより運動エネルギーを持っているのでしょうか。ボールがぶつかっても痛い程度で済みますが、これが車となるとそうはいきません。交通事故で命を落とすことさえあります。さらに、速いスピードで運動している物体ほど、ぶつかった衝撃は激しくなります。つまり、運動エネルギーは、物体の質量に比例し、物体の速さが速ければ速いほど大きくなります。
ちなみに、運動エネルギーは、物体の速さの2乗に比例する関係になります。速さが2倍になると、運動エネルギーは2の2乗倍の4倍、速さが3倍になると運動エネルギーは3の2乗倍の9倍にもなるのです。
❷物体の質量が大きいほど大きくなる。（質量に比例する）
❸物体の速さが速いほど大きくなる。（速さの2乗に比例する）
運動エネルギーの確認問題
質量1㎏の物体が10m/sで壁の釘にぶつかった場合、釘が1cm壁にめり込んだ。次の場合、釘は何cm壁にめり込むか。
（1）質量3㎏の物体が10m/sで壁の釘にぶつかったとき。
（2）質量1㎏の物体が30m/sで壁の釘にぶつかったとき。
（3）質量3㎏の物体が20m/sで壁の釘にぶつかったとき。
解答
（1）3cm
質量が3倍になっているので、運動エネルギーも3倍になります。
（2）9cm
速さが3倍になっているので、運動エネルギーは3の2乗倍になります。
（3）12cm
質量が3倍、速さが2倍になっているので、運動エネルギーは、3倍×2の2乗倍＝12倍になります。
運動エネルギーの計算方法
運動エネルギーは計算によっても求めることができます。詳しい内容は高校の物理で学習しますので、公式のみ紹介します。
運動エネルギー［Ｊ］＝1/2×質量［㎏］×速さ［ｍ/s］×速さ［m/s］
次は、位置エネルギーと運動エネルギーの和である力学的エネルギーについて学習します。
力学的エネルギー
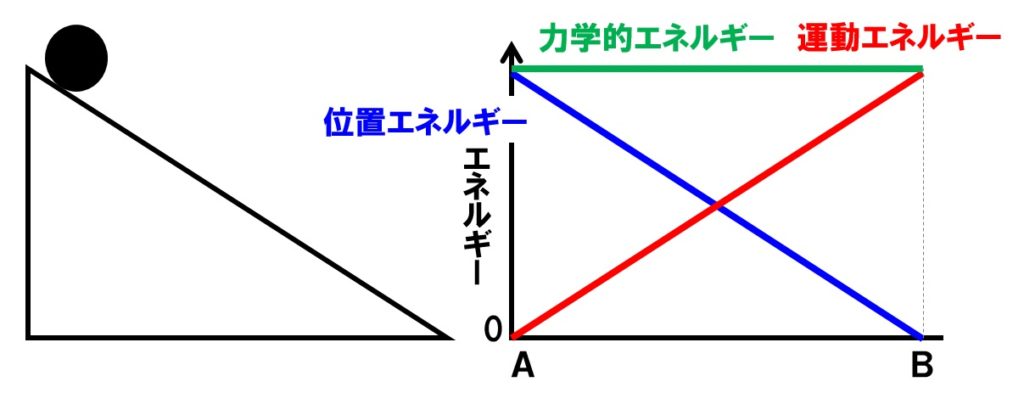
位置エネルギーと運動エネルギーの和を力学的エネルギーといいます。なぜこの2つのエネルギーを足すのかというと、ふりこの運動など、何かが落下するような運動の場合、この2つのエネルギーは互いに移り変わっているだけだからです。
したがって、物体が落下するにしたがって位置エネルギーは減少し、だんだん速くなり運動エネルギーが増加します。
力学的エネルギーの保存
位置エネルギーと運動エネルギーは互いに移り変わっているだけですので、空気の抵抗や摩擦がない場合は、その和は常に一定に保たれます。これを力学的エネルギーの保存（力学的エネルギー保存の法則）といいます。
空気の抵抗や摩擦がある場合は、力学的エネルギーが保存されません。一部が摩擦熱などに変わって空気中に熱エネルギーとして出ていってしまいます。ジェットコースターが同じ高さまで上がってこれないのはこのためです。
力学的エネルギーの保存の計算
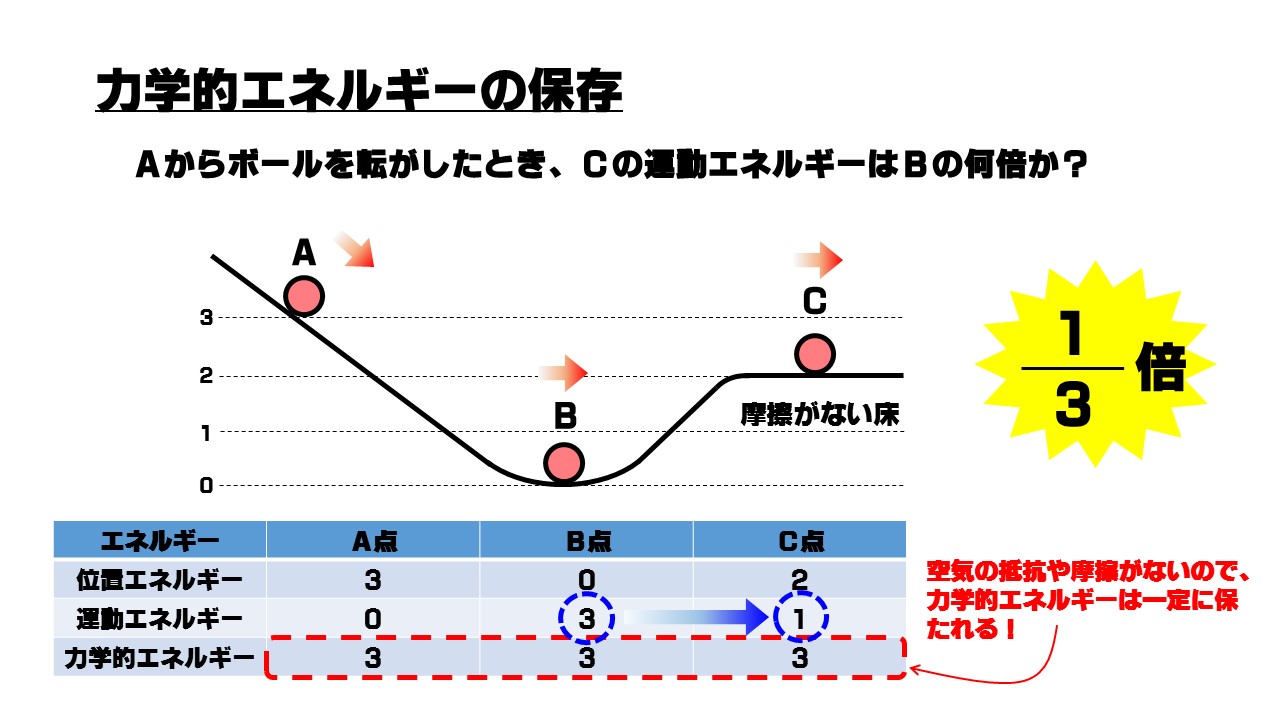
よく出題されるパターンが「〇点の運動エネルギーは△点の運動エネルギーの何倍？」という出題パターンです。何倍かを求めるので最後は割り算で求めます。
ここはミスがないようにしたいので、下図のような表を簡単に作って、各点の位置エネルギーと運動エネルギー、そしてその和である力学的エネルギーの値を勝手に書き込んでいきましょう。
- A点
高さが一番低いところからみて「高さ3」のところにあるので、勝手に位置エネルギーを3とします。ここから動き出すので運動エネルギーーは0です。その和である力学的エネルギーは3になります。 - B点
A点から転がってきて一番低いところに来ました。位置エネルギーが全て運動エネルギーに移り変わるので、位置エネルギーは0、運動エネルギーは3になります。力学的エネルギーは空気の抵抗や摩擦がないので3のまま変わりません。 - C点
高さが2のところまで上がってきたので、位置エネルギーは2、力学的エネルギーは3のまま変わらないはずなので、運動エネルギーは1となります。
【対策問題】力学的エネルギーの保存
図１は、ふりこの運動のようすを記録したもので、図２はこのときのおもりの持つ位置エネルギーの変化のようすをグラフに表したものである。これについて、次の各問いに答えなさい。ただし、ふりこはＡから振り下ろしたものとし、空気の抵抗や摩擦は考えないものとする。
（1）図１のＡ～Ｅの中で、おもりの速さが最大になるのはどれか。すべて選び記号で答えなさい。
（2）図１のＡ～Ｅの中で、おもりの速さが最小になるのはどれか。すべて選び記号で答えなさい。
（3）図１のA～Eの中で、おもりの持つ運動エネルギーが2番目に大きいのはどれか。すべて選び、記号で答えなさい。
（4）おもりが図１のＥ点に達したとき、ふりこの糸を切ると、おもりはその後どのように運動するか。次のア～エから選び、記号で答えよ。
ア 右斜め上に飛び出す。
イ 真横に飛び出す。
ウ 自由落下運動をする。
エ その場で静止する。
（5）図２のグラフは、おもりがＡ～Ｅまで運動したときの位置エネルギーの変化を表したものである。おもりがＡ～Ｅまで運動したときの運動エネルギーの変化のようすを、図２のグラフに表せ。
（6）位置エネルギーと運動エネルギーの和を力学的エネルギーという。ふりこがＡ～Ｅまで運動するときの、力学的エネルギーの変化をグラフに表すとどうなるか。図２のグラフに表せ。
（7）空気の抵抗や摩擦がない場合、力学的エネルギーは一定に保たれる。このことを何というか。
（8）図１のＡの基準面からの高さを30cm、Ｂの基準面からの高さを10cm、Ｃの基準面からの高さを0cmとすると、Ｃでの運動エネルギーはＢでの運動エネルギーの何倍になるか。
【解答・解説】力学的エネルギーの保存
（1）Ｃ
おもりの速さが最大になるのは、おもりの位置エネルギーが全て運動エネルギーに移り変わる最下点になります。
（2）Ａ、Ｅ
おもりの速さが最小になるのは、おもりの位置エネルギーが最大になり、運動エネルギーが最小になる点です。おもりの高さが一番高いところがこれにあたります。
（3）B、D
運動エネルギーは、おもりの速さが速いほど大きくなります。おもりがもっとも速いのは、最下点のCを通過するときで、次に速いのは、BとDを通過するときです。
（4）ウ
おもりが最高点に達したとき、おもりの速さが０になります。ここで、ひもを切ると、おもりは真下に自由落下運動をします。
（5）運動エネルギーのグラフは、位置エネルギーのグラフの正反対のかたちになります。
（6）空気の抵抗や摩擦がない場合、位置エネルギーと運動エネルギーの和である力学的エネルギーは一定に保たれます。
（7）力学的エネルギーの保存（力学的エネルギー保存の法則）
空気の抵抗や摩擦がない場合、位置エネルギーと運動エネルギーの和である力学的エネルギーは一定に保たれることを力学的エネルギーの保存といいます。
（8）1.5倍
Ａでの位置エネルギーを30とすると、運動エネルギーは0、その和である力学的エネルギーは30になります。Ｂでの位置エネルギーは10、力学的エネルギーは保存されるので30、したがって運動エネルギーは、30－10＝20。Ｃでの位置エネルギーは0、力学的エネルギーは保存されて30なので、運動エネルギーは、30－0＝30となります。Ｃでの運動エネルギーはＢでの運動エネルギーの、30÷20＝1.5倍になるとわかります。
コメント