【中3数学】三平方の定理の要点・練習問題

【中３数学】三平方の定理についてまとめています。入試では、なんらかの形でほぼ100％出題されるといって過言ではありません。しっかり学習してきましょう。

三平方の定理のポイント

直角三角形の直角をはさむ2辺の長さをa,b、斜辺の長さをcとすると、次の関係を成り立ちます。

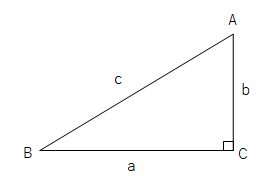
a²+b²=c²

これが三平方の定理です。

直角三角形の辺の長さ

直角三角形の2辺の長さがわかっているとき。三平方の定理を使うと残りの辺の長さを求めることができます。対角線を斜辺とする直角三角形に、三平方の定理をあてはめる問題も多いです。

三平方の定理の逆

△ABCで、BC=a CA=b AB=cとすると、a²+b²=c²ならば、∠C=90°となります。

直角三角形を探す問題

3辺の辺をそれぞれ2乗して考えます。

＜例＞5ｃｍ、7ｃｍ、8ｃｍの三角形は、直角三角形であるか。否か。
8²=5²+7²が成立しないので、違う。

また、辺の長さが小数や無理数であっても、a²+b²=c²が成り立てば、直角三角形です。

特別な角をもつ直角三角形

問題を解くうえでのポイント

1. 直角三角形の2辺の長さがわかれば、三平方の定理を使って、残りの辺の長さを求めることができる。
2. ただし、特別な角をもつ直角三角形の辺の比は、決まっているので、比例式を利用。
3. 正方形の対角線を引くと直角二等辺三角形や正三角形は、それぞれ45°、60°があるので、特別な角をもつ直角三角形の辺の比を利用。

三平方の定理の利用

弦や接線の長さ

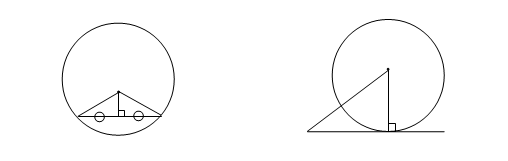
• 円の中心から弦にひいた垂線は、弦の中点を通ります。（左の図参照）
• 円外の1点から円にひいた接線は、その接点を通る半径と垂直になります。（右の図参照）

二等辺三角形と円

円の中心Ｏと弦の両端を結ぶと二等辺三角形となります。（半径はどこも同じ長さですね。）
二等辺三角形の頂点から底辺に引いた垂線は、底辺を2等分します。（垂直二等分線になっています。）

• 中心Ｏを頂点をする二等辺三角形を利用する問題として、頻出します。

具体例を通して学ぶ
下の図のように、半径8ｃｍの円Ｏで、中心Ｏからの距離が6ｃｍである弦ＡＢの長さをも求めよ。

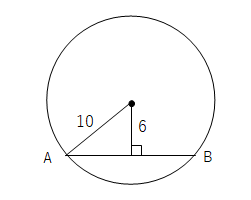
解説

1. 左側にできた直角三角形に注目して、残りの1辺を三平方の定理を利用して求めます。（特別な直角三角形の比3：4：5を使用しても可）
2. 求めたい長さをｘとすると。x²+6²＝10²　よってｘ＝8　（3：5＝6：ｘでも可）
3. 円の中心から弦にひいた垂線は、弦の中点を通るので、先ほどの長さを倍にして、8×2＝16ｃｍとなります。

三平方の定理の定期テスト対策問題

【問1】下の図の直角三角形で、ｘ値を求めよ。

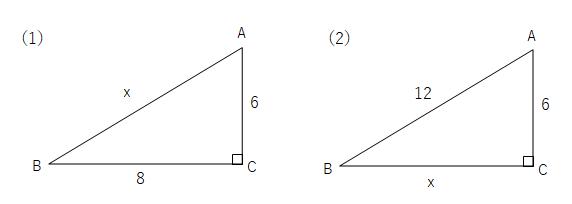
【問2】次の問いに答えなさい。

1. 2辺の長さが5ｃｍ、12ｃｍの長方形の対角線の長さを求めなさい。
2. 縦の長さが5ｃｍ、対角線の長さが11ｃｍの長方形の横の長さを求めなさい。

【問3】次の長さを3辺とする三角形のうち。直角三角形はどれですか。数字で答えよ。

1. 5ｃｍ、7ｃｍ、8ｃｍ
2. 12ｃｍ、16ｃｍ、20ｃｍ
3. 20ｃｍ、21ｃｍ、29ｃｍ
4. 10ｃｍ、15ｃｍ、20ｃｍ
5. 0.5ｃｍ、1.2ｃｍ、1.3ｃｍ
6. √3ｃｍ、√6ｃｍ、3ｃｍ

【問4】次のような長さから3つ選んで三角形をつくります。このとき。直角三角形になる組を2組答えなさい。ただし、3つの長さは、左から強い祭順に並べなさい。
（長さ）2　3　4　√5　√7　√10

【問5】次の問いに答えなさい。

1. 1辺が8ｃｍの正方形の対角線の長さを求めなさい。
2. 1辺が12ｃｍの正三角形の高さを求めなさい。

ヒント

• 正方形に対角線を引くと、直角二等辺三角形が2つできます。
• 正三角形（二等辺三角形）は、高さを下す（線をひく）と垂直二等分線となります。つま
• り、底辺の中点に、下した線がきます。底辺を半分ずつにしているところにきます。

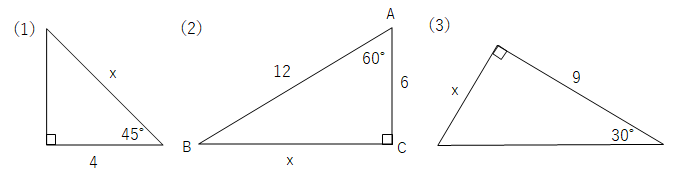
【問6】それぞれｘの値を求めなさい。

【問7】次の問いに答えなさい。

1. 半径12ｃｍの円Ｏで、中心Ｏからの距離が8ｃｍである弦ＡＢの長さを求めなさい。
2. ＡＢ＝ＡＣ＝13ｃｍの二等辺三角形△ＡＢＣがある。底辺であるＢＣ＝10ｃｍのとき、この二等辺三角形の高さを求めなさい。
3. 半径10ｃｍの円Ｏで、中心との距離が8ｃｍである弦ＡＢの長さを求めなさい。
4. 半径10ｃｍの円Ｏで、弦ＣＤの長さが8ｃｍのとき、中心と弦ＣＤの距離を求めなさい。

【問8】次の図で、直線ＡＢは点Ｂを接点とする円Ｏの接線です。次の問いに答えなさい。

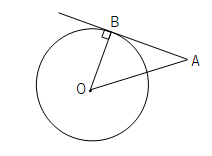
1. △ＯＡＢはどのような三角形か答えよ。
2. 円Ｏの半径4ｃｍ、線分ＯＡの長さを12ｃｍとするとき、接線ＡＢの長さを求めなさい。

三平方の定理の定期テスト対策問題解答

【問1】（1）10　（2）6√3
【問2】（1）13　（2）4√6
【問3】2、3、5、6
【問4】（2、√5、3）　（√7、3、4）
【問5】（1）8√2　（2）6√3
【問6】（1）4√2　（2）4√3　（3）3√3

【問7】

1. 8√5ｃｍ
2. 12ｃｍ
3. 12ｃｍ
4. 2√21ｃｍ

【問8】

1. 直角三角形
2. 8√2ｃｍ

入試では、複雑な図形の中で、その特別な角をもつ直角三角形を探したり、問題の条件を読む中で、角度を知り、「特別な角をもつ直角三角形の辺の比」を使用させたりさせる問題が多いです。演習を重ね、習得しましょう。ただし、どの都道府県でも大問1にあるような小問集合の問題には、今回のような分かり切った状態で出題され、「特別な角をもつ直角三角形の辺の比」を使わせる問題も出題されるケースもあります。そのときは、しっかり得点していくことが大切となります。