【高校受験対策数学】円周角の角度を求める練習問題

【高校受験対策数学】円周角の角度を求める練習問題です。

【問題】円周角の角度を求める練習問題

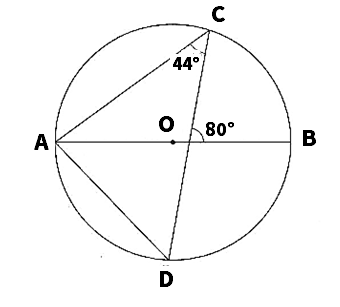
（1）次の図において、線分ABは円0の直径であり2点CDは円Oの周上の点である。このとき、∠ADCの大きさを求めよ。

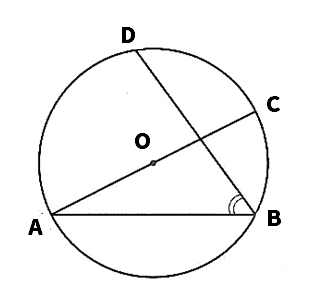
（2）次の図のように、円0の周上に4点A、B、C、Dがあり、線分ACは点Oを通る。点Bを含まない弧ADの長さと点Bを含まない弧DCの長さの比が3:2のとき、∠ABDの大きさを求めよ。

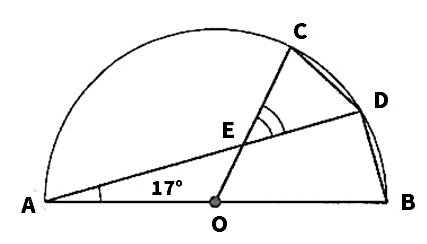
（3）次の図で、C、DはABを直径とする半円Oの周上の点で、CD=DBである。また、Eは線分DAとCOとの交点である。∠EAO=17°のとき、∠CEDの大きさを求めよ。

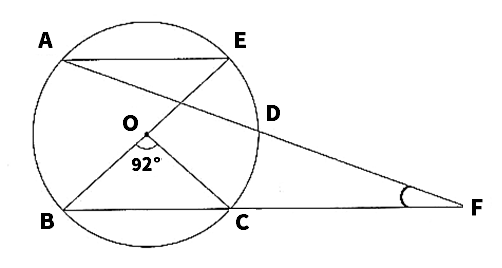
（4）次の図で、5点A、B、C、D、EはBEを直径とする円0の周上にあり、AE//BC、弧CD=弧DEである。直線ADと直線BCの交点をFとする。このとき、∠AFBの大きさを求めよ。

（5）次の図のように、円0の外の点Pから中心Oを通る直線をひき、円との交点を点Pに近い方からそれぞれ点A、Bとする。また、点Pから円Oに接線を1本ひき、その接点を点Cとする。さらに、点Bからこの接線に垂線をひき、円との交点をD、接線との交点をEとする。∠APC=32°のとき、∠DCEの大きさxを求めよ。

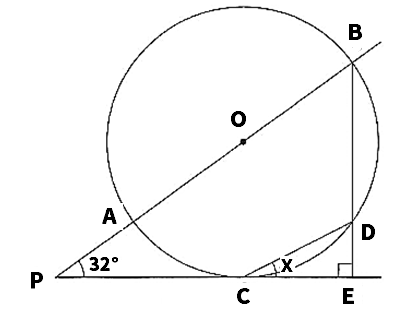
【解答・解説】円周角の角度を求める練習問題

（1）54°
三角形の内角と外角の関係より、∠BAC＝80°-44°＝36°
円周角の定理より、∠BDC=∠BAC=36°
半円の弧に対する円周角だから、∠BDA=90°
よって、∠ADC=∠BDA−∠BDC=90°-36°＝54°

（2）54°
∠ABD＝1/2∠AOD＝1/2×（3/5×180）＝54°

（3）51°
DとOを結ぶ。
∠DOB=2∠EAO=34°
CD=DB、より∠COD=∠DOB=34°
△EODの内角と外角の関係より、
∠CED＝∠EOD+∠EDO=34°÷17°=51°

（4）22°
AE//BFより、錯角は等しいから、∠AFB=∠FAE
円周角の定理より、∠FAE=∠DBE
弧CD=弧DEより、∠DBE=1/2∠CBE=1/2×1/2×(180°-92°)=22°

（5）29°
OとC、OとDを結ぶ。
∠PCO=90°より、OC//BE
∠POC=∠PBE=180°-(32°+90°)=58°