【中1数学】図形の定期テスト対策問題です。
基本的な定理や公式を確認しながら、1問1問丁寧に解くことが大事です。おうぎ形や空間図形の計量では、公式を使えるように問題を解きながらマスターしていきましょう。
【問題】図形の定期テスト対策問題(中1数学)
【1】おうぎ形
次の図のおうぎ形について、(1)は弧の長さを、(2)、(3)は面積を求めなさい。
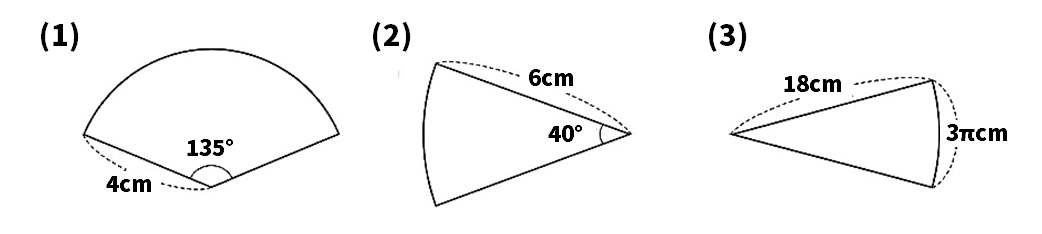
【2】直線や平面の位置関係
次の図の三角柱ABC-DEFにおいて、辺ACとねじれの位置にある辺をすべて答えなさい。
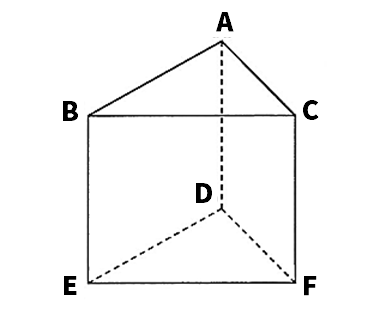
【3】立体の体積と表面積
次の(1)円柱(2)球(3)正四角錐の立体の体積と表面積を求めなさい。
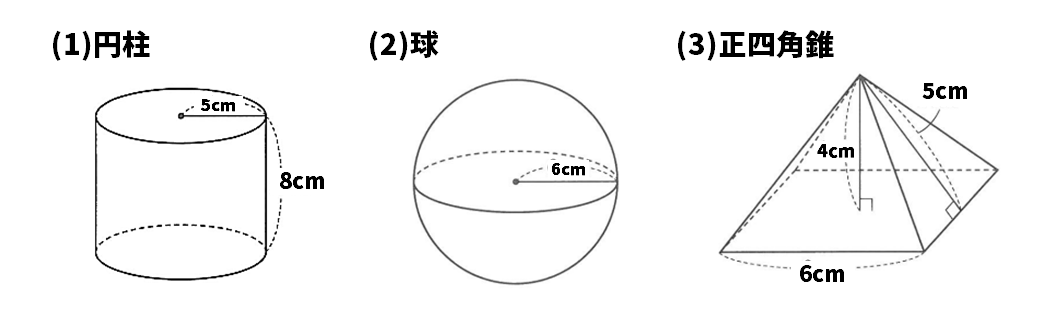
【解答・解説】図形の定期テスト対策問題(中1数学)
(1)37πcm
半径r、中心角aのおうぎ形の弧の長さをℓとすると、ℓ=2πr×a/360と表される。
これにr=4、a=135を代入して計算すると、37π(cm)
これにr=4、a=135を代入して計算すると、37π(cm)
(2)4πcm2
半径r、中心角aのおうぎ形の面積をSとすると、S=r2π×a/360と表される。
これにr=6、a=40を代入して計算すると4π(cm2).
これにr=6、a=40を代入して計算すると4π(cm2).
(3)27πcm2
半径r、弧の長さℓのおうぎ形の面積をSとすると、S=1/2ℓrと表される。
これにr=18、ℓ=3πを代入して計算すると27π(cm2).
これにr=18、ℓ=3πを代入して計算すると27π(cm2).
【2】辺BE、辺DE、辺EF
辺ACと平行でなく、交わらない辺を答える。辺ACと平行な辺は辺DF、辺ACと交わる辺は辺AB、辺BC、辺AD、CFだから、辺ACとねじれの位置にある辺は、辺BE、辺DE、辺EFである。
【3】
(1)体積:200πcm3、表面積:130πcm2
角柱・円柱の体積=(底面積)×(高さ)、角柱・円柱の表面積=(側面積)+(底面積)×2である。
底面積は、π×52=25π(cm2)よって、体積は25π×8=200π(cm3)。
側面積は、8×(2π×5)=80π(cm2)よって、表面積は80π+25π×2=130π(cm2).
底面積は、π×52=25π(cm2)よって、体積は25π×8=200π(cm3)。
側面積は、8×(2π×5)=80π(cm2)よって、表面積は80π+25π×2=130π(cm2).
(2)体積:288πcm3、表面積:144πcm2
半径rの球の体積をV、表面積をSとすると、V=4/3πr3、S=4πr2と表される。
それぞれ、r=6を代入して計算する。
それぞれ、r=6を代入して計算する。
(3)体積:48cm3、表面積:96cm2
角錐・円錐の体積=1/3×(底面積)×(高さ)
角錐・円錐の表面積=(側面積)+(底面積)である。
底面積は、6×6=36(cm)だから、体積は、1/3×36×4=48(cm2)。
側面積は、1/2×6×5=15×4=60(cm2)だから表面積は60+36=96(cm2).
角錐・円錐の表面積=(側面積)+(底面積)である。
底面積は、6×6=36(cm)だから、体積は、1/3×36×4=48(cm2)。
側面積は、1/2×6×5=15×4=60(cm2)だから表面積は60+36=96(cm2).


コメント