浮力についての問題演習を行います。浮力の計算方法はいくつかありますが、すべてのパターンを演習できるようになっています。
浮力の確認問題
- 水などの液体の中で、物体が上向きに受ける力を何というか。
- 浮力の大きさは、液体の中にある物体の体積が大きくなるとどうなるか。
- 浮力が生じるのは、液体の中にある物体の上面と下面にはたらく何の差が原因か。
- 物体が完全に液体の中にある場合、物体の深さをさらに深くすると、浮力の大きさはどうなるか。
- 質量500gの物体をばねばかりにつるし、液体の中に沈めると、ばねばかりは4.0Nを示した。このときの浮力の大きさは何Nか。ただし、100gの物体にはたらく重力の大きさを1.0Nとする。
- 質量400gの物体が水に浮かんでいるとき、物体にはたらく浮力の大きさは何Nになるか。
解答
- 浮力
- 大きくなる
- 水圧
- 変わらない
- 1.0N ※5.0N－4.0N＝1.0N
- 4.0N
【練習問題❶】圧力と浮力
［問題］図１のように、ばねはかりに底面積が20cm²の物体をつるすと1.5Ｎを示した。このときばねののびは6.0cmであった。次に、この物体を図２のようにばねはかりにつるしたまま水にしずめたところ、ばねはかりは1.0Ｎを示した。これについて、次の問いに答えよ。ただし、100gの物体にはたらく重力の大きさを1.0Nとし、空気の重さは考えないものとする。
（1）図１で、ばねはかりが1.5Nを示したことから、物体の質量は何gだとわかるか。
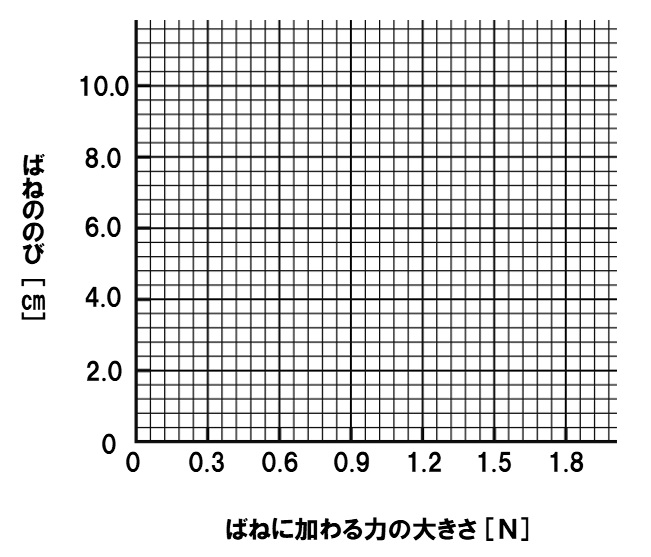
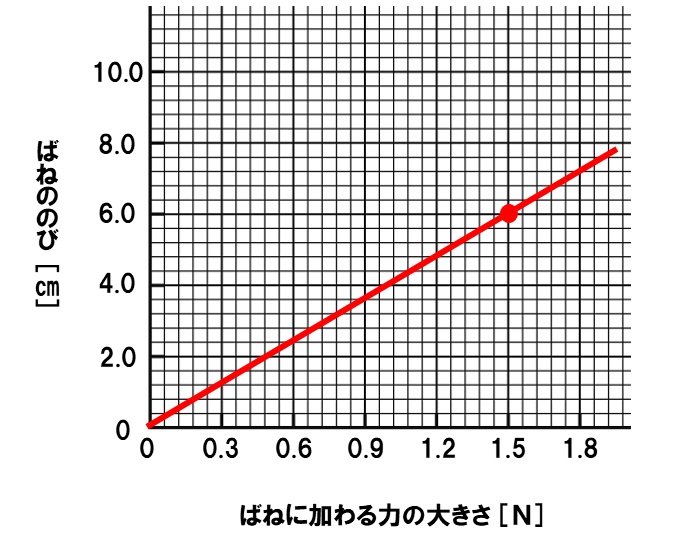
（2）実験で使用したばねについて、ばねに加わる力の大きさとばねののびの関係を、したのグラフに表せ。
（3）図１の物体をばねはかりからはずし、床の上に静かにおいた。このとき、物体が床にあたえる圧力は何Paか。
（4）図２で、物体を水に沈めたとき、物体には重力のほかに浮力がはたらいていると考えられる。この浮力の大きさは何Nか。
（5）物体が完全に水につかっている場合、物体をさらに深く沈めた場合、水の中で物体が受ける浮力の力の大きさはどうなるか。簡潔に書け。
【解答・解説❶】圧力と浮力
（1）150g
100gの物体にはたらく重力の大きさが1.0Nなので、1.5N＝150gとなります。
（2）ばねののびは、ばねに加わる力の大きさに比例します。なので、原点を通る直線になります。1.5Nで6.0cmののびであったことから、グラフは下のようになります。
（3）750Pa
１Pa＝１N/㎡なので、1㎡あたりの力の大きさを計算すればいいのです。底面積が20㎠なので、㎡に変換すると、
20㎠＝0.002㎡
したがって圧力N/㎡（Pa）は、
1.5N÷0.002㎡＝750Pa
になります。
（4）0.5N
浮力の求め方は、
空気中でのばねはかりの値ー水中でのばねはかりの値
で求めることができます。したがって浮力の大きさは、
1.5N－1.0N＝0.5N
となります。
（5）変化しない。
水の中にある物体にはたらく浮力は、水につかっている物体の体積で決まります。物体が全て水につかっている場合、さらに深く沈めようが、物体が水につかっている体積は変化しませんので、浮力の大きさも変化しません。
【練習問題❷】浮力の計算
［問題］下の図のように、質量800gの物体Aをばねはかりにつるし、全体が水につかり、ビーカーの底に物体Aぐ触れないように静かに水の中に沈めた。質量600gの物体Bも、物体Aと同じようにビーカーの水に入れたところ、物体Bが水面から少し飛び出した状態で静止した。これについて、次の各問いに答えなさい。ただし、100gの物体にはたらく重力を1.0Nとする
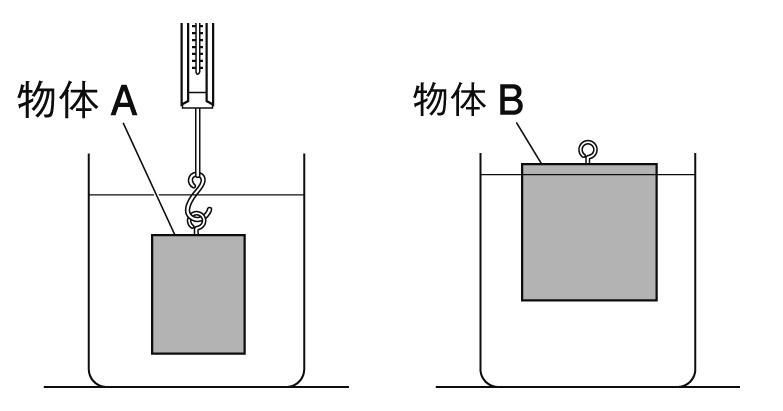
（1）図のように物体Aを水中に沈めたところ、物体Aを支えるばねはかりは5.0Nを示していた。このとき、物体Aにはたらく浮力大きさは何Nか。
（2）物体Aを図の状態から、ビーカーの底につかないようにさらに深く沈めた場合、ばねはかりの示す値はどうなるか。次のア～エの中から一つ選び、記号で答えよ。
ア ばねはかりの示す値は小さくなる
イ ばねはかりの示す値は大きくなる
ウ ばねはかりの示す値は変化しない
エ ばねはかりの示す値は不規則に変化する
（3）図のように物体Bが水面に浮かんでいるとき、物体Bにはたらく浮力の大きさは何Nか。
（4）図の状態の物体Bを、すべて水中につかるように手で押さえたとき、物体Bにはたらく浮力の大きさと重力の大きさは、それぞれどうなるか。簡潔に答えよ。
【解答・解説❷】浮力の計算
（1）3.0N
浮力の大きは、次の式で求めることができます。
浮力＝空気中でのばねはかりの値ー水中でのばねはかりの値
物体Aの質量は800gなので、800g＝8.0N
8.0N－5.0N＝3.0N
となります。
（2）ウ
浮力の大きさは、水中にある物体の体積で決まります。物体Aはすでに全体が水につかっているので、深くなろうが浅くなろうが、物体がすべて使っている状態なら、浮力の大きさは変化しません。
（3）6.0N
物体Bは水面に浮いて静止しています。静止しているということは、物体Bにはたらく力がつり合っているということです。つまり、物体Bにはたらく重力と浮力が同じ大きさで、つり合った状態になっています。
物体Bは600gなので、600g＝6.0N
物体Bにはたらく重力が6.0Nなので、浮力の大きさも6.0Nになります。
（4）浮力：大きくなる 重力：変化しない
物体Bは最初の状態では、全体が水に浸かっていません。この状態から全て水に浸かるように沈めると、水中にある物体の体積が大きくなり、浮力が大きくなります。重力は、地球が物体を引く力で、物体がどんな状態にあろうが変化しません。
【練習問題❸】浮力とグラフ
浮力の大きさを調べるために、下の図１のように物体をビーカーの水の中に入れる実験を行った。図２は、水面から物体の底面までの距離と、ばねばかりが示した値を表したグラフである。これについて、以下の各問いに答えよ。ただし、100gの物体にはたらく重力の大きさを1.0Nとする。
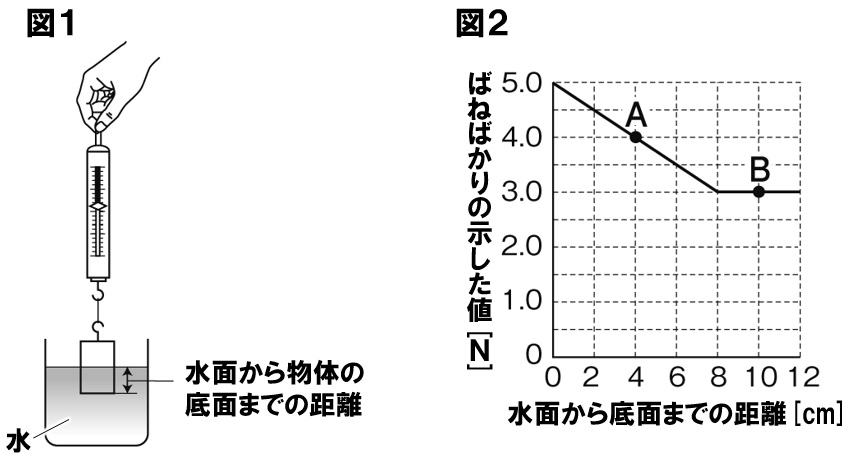
（1）この物体の質量は何gか。
（2）この物体を空気中から水の中に沈めていき、図２のグラフのA点になったとき、この物体にはたらく浮力の大きさは何Nになるか。
（3）この物体の高さは何cmか。
（4）この物体をさらに水の中に沈めていき、図２のグラフのB点になったとき、この物体にはたらく浮力の大きさは何Nか。
（5）次の文は、この実験からわかる浮力の大きさについてまとめたものである。文中の（ ）に適する語句を入れなさい。
【解答・解説❸】浮力とグラフ
（1）500g
図２のグラフで、水面から物体の底面までの距離が0cm（まだ水につかっていない）のとき、ばねばかりは5.0Nを示すことから、この物体の重さは5.0Nであるとわかります。100gの物体にはたらく重力大きさが1.0Nなので、この物体の質量は500gであるとわかります。
（2）1.0N
図２のグラフのA点は、水面から物体の底面までの距離が4cmのときで、このときばねばかりは4.0Nを示しています。物体の重さは5.0Nだったので、
5.0N－4.0N＝1.0N
の浮力が生じていることがわかります。浮力の分だけ、ばねばかりの値は小さくなります。
（3）8.0cm
浮力の大きさは、水中にある物体の体積によって決まります。物体が完全に水中につかった場合、深かろうが浅かろうが浮力の大きさは変化しません。したがって、ばねばかりの示す値が変化しなくなる8.0cmが物体の高さになります。
（4）2.0N
浮力の大きさを求めるので、（2）の解き方と同じになります。グラフのB点のとき、ばねばかりは3.0Nを示しているので、
5.0N－3.0N＝2.0N
の浮力が生じていることがわかります。
（5）①体積 ②変わらない
【発展理科問題】アルキメデスの原理
右図のような、質量60.0g、底面積2.0cm²、高さ4.0cmの円柱の金属をばねばかりにつるして液体の中に沈めていく実験を行った。このとき、円柱の下の底面と液面との距離ｈ〔cm〕とばねばかりの示す値ｍ〔g〕は、下の表のようになった。これについて、後の各問いに答えよ。ただし、100gの物体にはたらく重力の大きさを1.0Nとする。
| ｈ〔cm〕 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 |
| ｍ〔g〕 | 57.6 | 55.2 | 52.8 | 50.4 | 50.4 |
（1）ｈ〔cm〕が4.0cmよりも小さいとき、ばねばかりが示す値ｍをｈを用いて答えよ。
（2）円柱の金属にはたらいている重力の大きさは何Nか。
（3）金属がすべて液体中に沈んだとき、液体から受ける浮力の大きさは何Nか。
（4）「浮力は押しのけた液体の重さに等しい」という原理がある。上の実験の結果から液体の密度は何g/cm³であるとわかるか。
【発展 解答・解説】アルキメデスの原理
（1）ｍ＝60－2.4ｈ
表より、ｈ＜４のとき、円柱の金属を1cm沈めるごとにｍ〔g〕は2.4gずつ小さくなっていることがわかります。このことから、ｈ〔cm〕金属を沈めると、ｍ＝60－2.4ｈと表すことができます。
（2）0.6N
円柱の金属の質量は60gで、100gの物体にはたらく重力の大きさが1.0Nなので、
60g＝0.6N
になります。
（3）0.096N
円柱の金属が完全に液体中に沈んだとき、ばねばかりの示す値ｍ〔g〕は50.4gになっています。物体の質量は60.0gなので、液体中では、ばねばかりの示す値が、
60.0g－50.4g＝9.6g
小さくなっていることがわかります。したがって、浮力の大きさは、
9.6g＝0.096N
になります。
（4）1.2g/cm³
まずは、液体中の金属の体積を求めます。金属はすべて液体につかっているので、
2.0cm²×4.0cm＝8.0cm³
押しのけられた液体の体積も8.0cm³になります。その重さが0.096Nになるので、液体の密度は、
0.096N＝9.6g
9.6g÷8.0cm³＝1.2g/cm³
となります。
コメント