【中1理科】焦点距離の求め方＆ポイントを徹底解説！よく出る問題付き

凸レンズの問題で焦点距離を求めさせる問題が出題されます。焦点距離の２倍の位置、作図、公式を使った求め方がありますのでそれらを紹介します。

焦点距離の求め方

焦点距離を求めさせる問題は次の3つのパターンに分類されます。

特に高校入試でよく問われるのが、❶の焦点距離2倍の位置の関係を利用するパターンです。

焦点距離の2倍の位置

焦点距離の2倍の位置に光源を置くと、光源と同じ大きさの実像が、焦点距離の2倍の位置にできます。

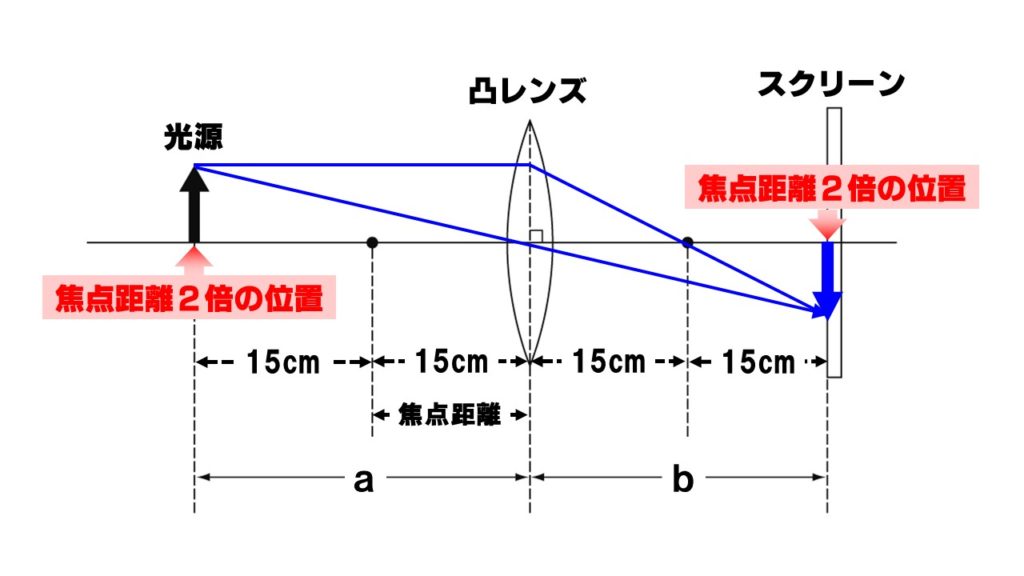
上の図で説明すると、光源が焦点距離の2倍の位置に置いてあります。焦点距離2倍の位置ですから、凸レンズの中心から焦点までの距離（焦点距離）と、焦点から光源までの距離が等しくなっています。

このとき、実像ができるのはこちらも焦点距離の2倍の位置になります。凸レンズの中心から光源までの距離をａ、凸レンズの中心からはっきりとした実度像が映ったスクリーンまでの距離をｂとすると、ａ＝ｂという関係が成り立ちます。

上の図の場合、ａの距離が30cm、ｂの距離が30cmと等しくなっているので、焦点距離は、
30cm÷2＝15cm
であると計算できます。

作図で求めるパターン

焦点を作図させ、凸レンズの中心から焦点までの距離を測らせる問題も出題されます。作図の方法は次の通りです。

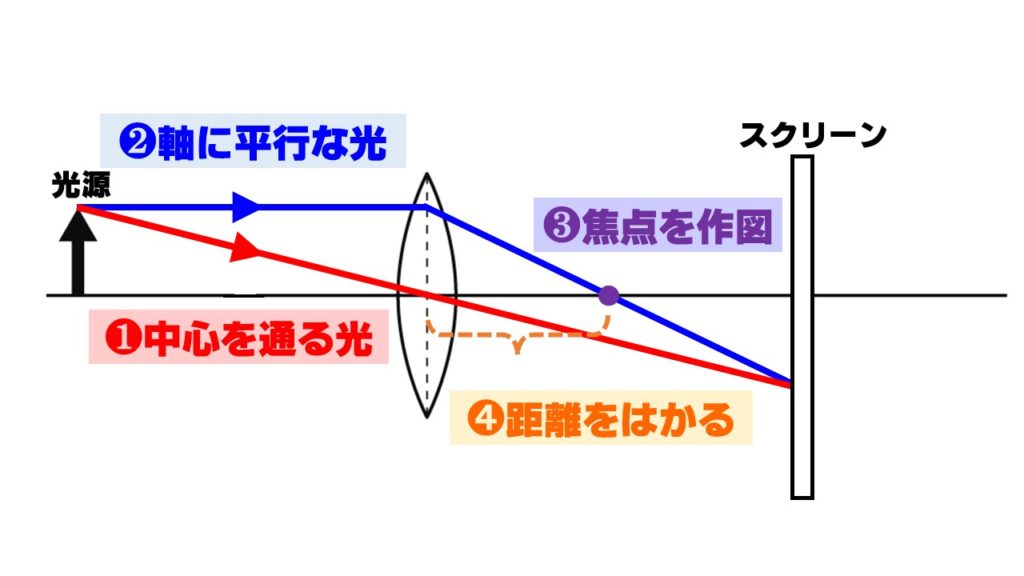
• ❶レンズの中心を通過する光　→　直進させる
• ❷軸に平行な光　→　レンズの中心線で屈折させスクリーン上で❶の光と交わらせる
• ❸❷の光が軸を通ったところに焦点を作図
• ❹凸レンズの中心から焦点までの距離を測る

公式で計算する方法

焦点距離の便利な公式も覚えておいても損はないでしょう。

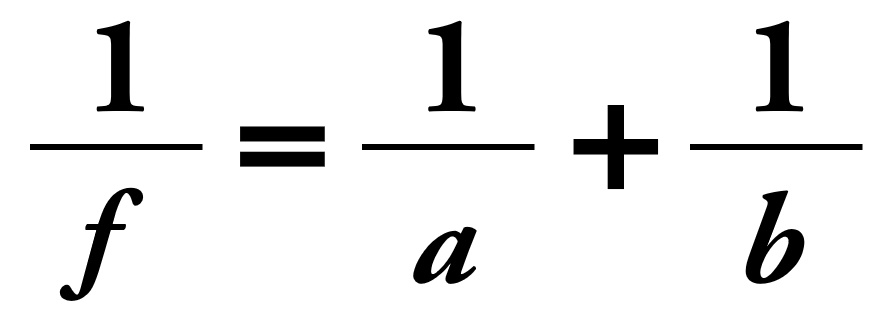
※ｆは焦点距離
※ａは凸レンズの中心から光源までの距離
※ｂは凸レンズの中心からスクリーンまでの距離

下の図で焦点距離の公式を実際に使ってみましょう。

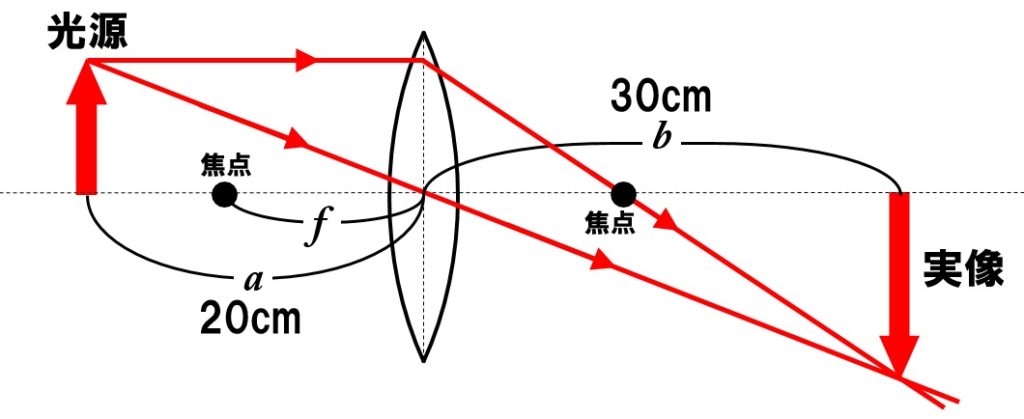
焦点距離の公式に、a＝20、b＝30を代入すると、
1/f = 1/20 + 1/30
1/f = 3/60 + 2/60
1/f = 5/60
1/f = 1/12
したがって、焦点距離は12cmとなります。

【対策問題】焦点距離の求めさせる問題

［問題］下の図のように、光学台に凸レンズとスクリーン、厚紙を取り付けた電球をセットし、厚紙を取り付けた電球の位置を変えながら、スクリーンにはっきりとした像ができるようにスクリーンの位置を調節した。このとき、凸レンズと厚紙を取り付けた電球の位置までをａcm、凸レンズとスクリーンまでをｂcmとして、下の表に記録した。これについて、次の各問いに答えよ。

（1）表の結果から、この凸レンズの焦点距離を求めよ。

（2）表のA～Fの像のうち、物体よりも大きいものはどれか。すべて選び、記号で答えよ。

（3）厚紙を取り付けた電球を、ある距離以上に凸レンズに近づけると、スクリーンに像ができなくなった。何cm以上近づけるとスクリーンに像ができなくなるか。

（4）表のCのとき、凸レンズの上半分を黒い紙でおおった。このとき、スクリーンにできる像の明るさと大きさはどうなるか。次のア～カから一つ選び、記号で答えよ。
ア　像の明るさは変わらないが、像の上半分がスクリーンにうつらなかった。
イ　像の明るさは変わらないが、像の下半分がスクリーンにうつらなかった。
ウ　像の明るさは暗くなり、像の上半分がスクリーンにうつらなかった。
エ　像の明るさは暗くなり、像の下半分がスクリーンにうつらなかった。
オ　像の明るさは暗くなり、像の大きさが半分になった。
カ　像の明るさは暗くなるが、大きさは変わらず像が欠けたりしなかった。

【解答・解説】焦点距離の求めさせる問題

（1）10cm

光源を焦点距離の2倍の位置に置いた場合、光源の大きさとできる実像の大きさが等しくなり、凸レンズと光源、凸レンズと実像ができる位置までの距離が等しくなります。したがって、表でａとｂの距離が等しくなっているＣの20cmが焦点距離2倍の位置になります。焦点距離は、20cm÷2＝10cmとなります。

（2）D、E、F

焦点距離の2倍の位置よりも、凸レンズに近い位置に光源を置いた場合、スクリーンにできる実像の大きさは光源の大きさよりも大きくなります。表で焦点距離の2倍の位置がCなので、それよりもａが短いＤ、Ｅ、Ｆのとき、光源よりも大きい実像が観察されます。

（3）10cm

焦点距離が（1）で10cmとわかったので、それ以上に光源を凸レンズに近づけると実像がスクリーンにできなくなります。焦点上に光源を置いた場合は、実像も虚像も観察できなくなり、焦点よりも内側に光源を置いた場合、凸レンズ越しに虚像が観察できるようになります。

（4）カ

凸レンズの上半分や下半分を黒い紙でおおっても、レンズのおおっていない方から光が屈折して進むので、実像が欠けたり、大きさが小さくなったりすることはありません。ただし、凸レンズを通過して集まる光の量が少なくなるので、その分実像の明るさは暗くなります。