太陽や星の動きで登場する透明半球について学習します。南中時刻や昼の長さを計算したりできるようになりましょう。
透明半球の計算問題
透明半球とは、天球を模型にしたもので、この透明半球を使って太陽の一日の動きを記録することができます。その中でも今日は南中時刻や日の出日の入りの時刻の計算方法を練習します。
時間と太陽の移動距離は比例関係
時間と太陽が透明半球上を移動した距離は比例の関係になります。時間が2倍になれば、太陽が動いた距離ももちろん2倍になります。ということは比例式を立てると、南中時刻などを計算することができます。
例えば、太陽が透明半球上を1時間で2cm移動したとします。4cm移動するには何時間かかりますか?と言われたらすぐに答えは計算できますよね。
1時間:2cm=x時間:4cm
2x=4
x=2時間
このように計算すれば南中時刻や日の出日の入りの時刻も計算できます。
太陽の南中時刻の計算問題1
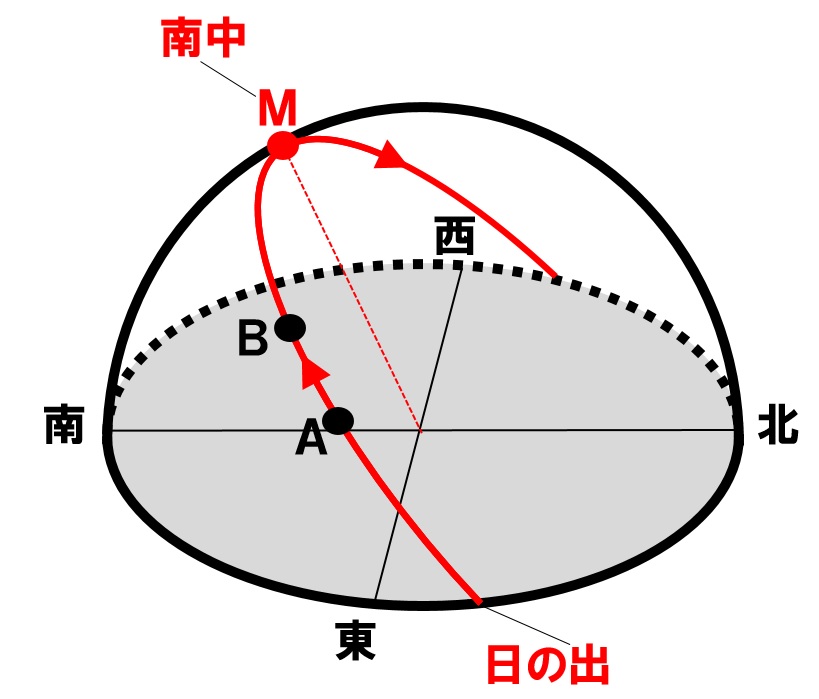
[例題]下の図のように、太陽の一日の動きを透明半球に記録した。Aは午前9時に太陽の位置を記録したものであり、Bはその1時間後に太陽の位置を記録したものである。AといBの長さをはかると2.4cmであった。また、Mは太陽が真南に来たときの記録で、BM間の長さは7.2cmであった。この日の太陽の南中時刻を求めなさい。
解答・解説
まずは計算しやすい数字にしています。計算の流れを確認しましょう。その前に、文章中に登場した時刻や長さを図に書き込みます。
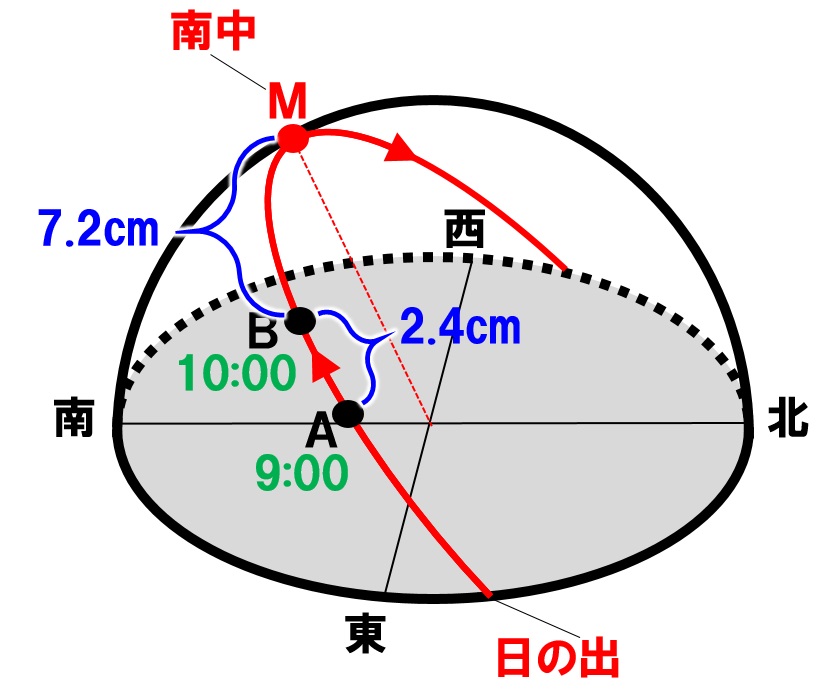
太陽の動いた距離と時間が比例していることを使って、比例式を立てて計算していきます。
- 1時間:2.4cm=x時間:7.2cm
2.4x=7.2
x=3時間 - 午前10:00+3時間=午後1時
簡単ですね。次は少し計算がややこしくなります。
太陽の南中時刻の計算問題2
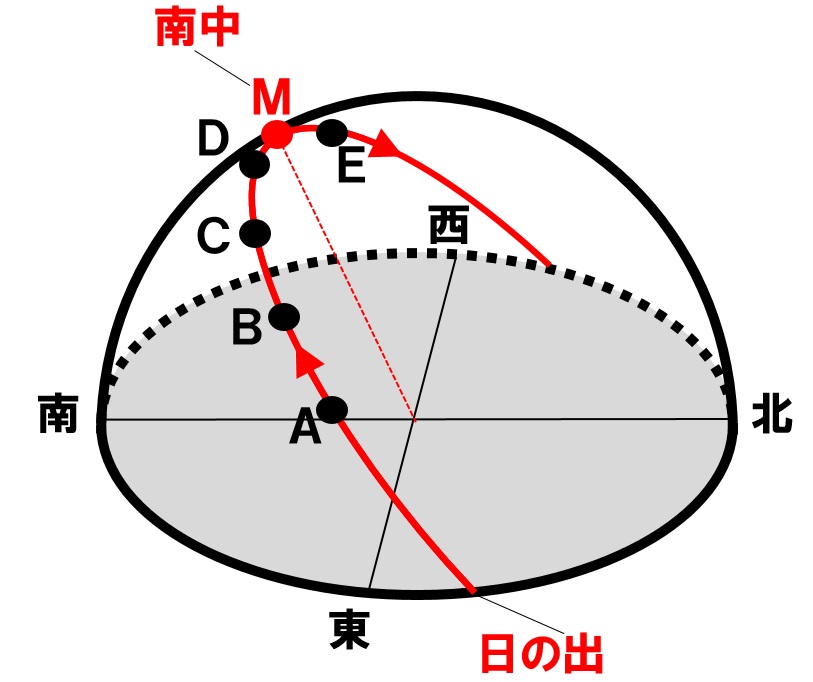
[例題]下の図のように、太陽の一日の動きを透明半球に記録した。Aは午前9時に太陽の位置を記録したものであり、その後1時間ごとにBからEの太陽の位置を記録した。Mは太陽が真南に来たときの記録で、DM間の長さは0.4cmであった。この日の太陽の南中時刻を求めなさい。
解答・解説
まずは計算しやすい数字にしています。計算の流れを確認しましょう。その前に、文章中に登場した時刻や長さを図に書き込みます。
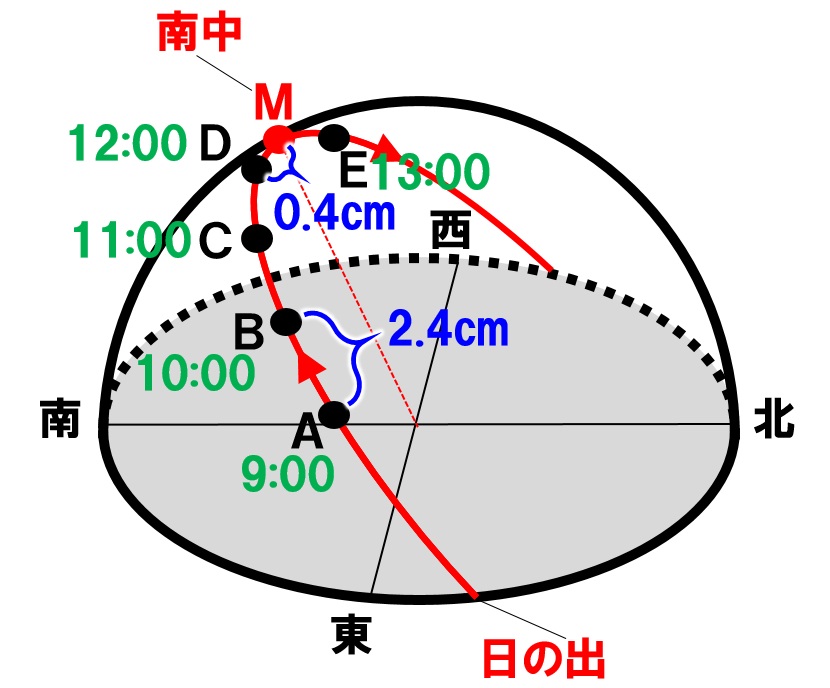
太陽の動いた距離と時間が比例していることを使って、比例式を立てて計算していきます。
- 1時間:2.4cm=x時間:0.4cm
2.4x=0.4
x=1/6時間 - 1/6時間×60=10分
- 午前12:00+10=午前12時10分
時間を分にするのが苦手な生徒は1時間を60分に直してから計算します。
- 60分:2.4cm=x分:0.4cm
2.4x=24
x=10分 - 午前12:00+10=午前12時10分
それでは、下のリンク先で実際の問題に挑戦しましょう。


コメント