中学1年理科。今日のテーマは圧力です。圧力とは何なのか。圧力の計算の仕方はどうすればいいのかをマスターしましょう。ここは苦手な生徒が多いので、しっかりと練習し差をつけていきましょう。問題演習もしっかりできるように多彩な問題を準備しています。
圧力とは
圧力とは、単位面積(1m²や1cm²)あたりの力の大きさです。物体に力を加えるとき、力が加わっている面積によって、物体のへこみ具合などに差が生じます。このように、力が加わる面積も考えた力の大きさを圧力といいます。
圧力の計算方法
圧力を表す単位は、中学校では4つ登場します。単位面積が異なりますので、注意してください。
❶N/cm²
N/cm²(ニュートン毎平方センチメートル)と読みます。その単位の通り、1cm²あたりに何Nの力が加わっているかを表しています。計算方法は次の通りです。
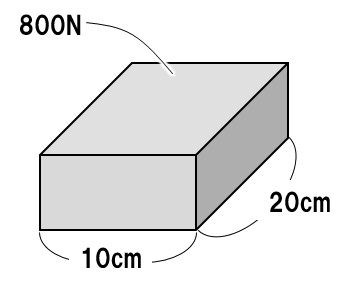 Q:右の図の物体が床に加える圧力は何N/cm²か?
Q:右の図の物体が床に加える圧力は何N/cm²か?
A:800N÷200cm²=4N/cm²
❷N/m²
N/m²(ニュートン毎平方メートル)と読みます。これも単位の通り、1m²あたりに何Nの力が加わっているかを表します。計算方法は次の通りです。
 Q:右の図の物体が床に加える圧力は何N/m²か?
Q:右の図の物体が床に加える圧力は何N/m²か?
A:800N÷0.02m²=40000N/m²
❸Pa
Pa(パスカル)と読みます。PaはN/m²と同じ圧力の大きさを表す単位です。つまり、1N/m²=1Paになります。したがって計算方法も次の通りになります。
 Q:右の図の物体が床に加える圧力は何Paか?
Q:右の図の物体が床に加える圧力は何Paか?
A:800N÷0.02m²=40000Pa
❹hPa
hPa(ヘクトパスカル)と読みます。hPaのhは「ヘクト」という補助単位で、「100」という意味があります。つまり、1hPa=100Paになるのです。
N/cm²とN/m²(Pa)の関係
この2つの圧力は、単位面積が1cm²と1m²と異なります。
1m²=1m×1m=100cm×100cm=10000cm²
単位面積が10000倍違うのです。したがって、N/cm²とN/m²(Pa)には次のような関係があります。
- 1N/cm²=10000N/m²(Pa)
この関係を知っていると、N/cm²からN/m²(Pa)への変換が非常に早くなります。N/cm²を求めて10000倍するだけでいいのです。
圧力と力の大きさや面積
圧力と力の大きさや面積にはどのような関係があるのでしょうか。力の大きさ(重さ)や面積が変わると、圧力がどう変化するか見ていきましょう。
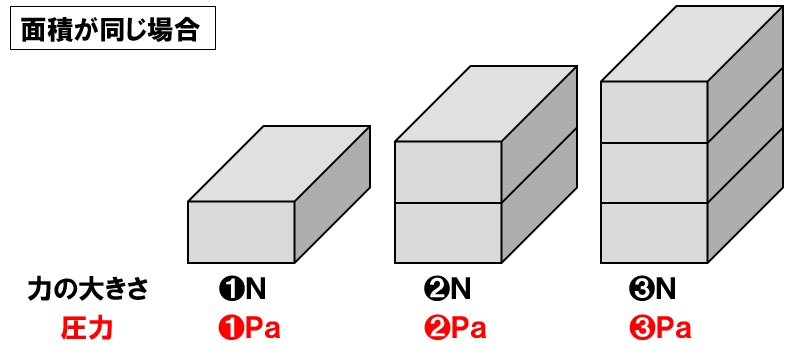
圧力と力の大きさ
力が加わる面積が変化しない場合、力の大きさを2倍にすると、圧力も2倍になります。つまり力の大きさと圧力は比例するのです。
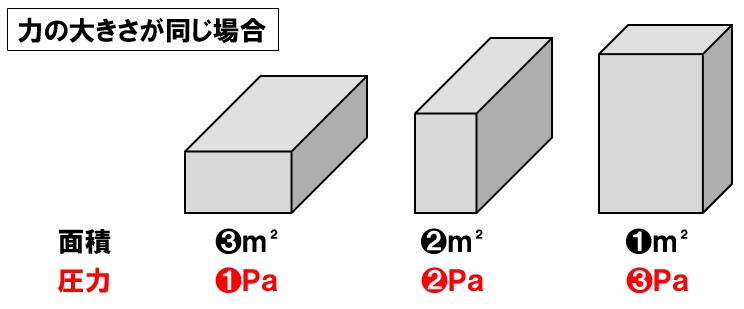
圧力と面積
物体に加える力が変化しない場合、面積を2倍にすると、圧力は1/2になります。つまり面積と圧力は反比例の関係になるのです。
圧力と面積の関係を利用した道具もテストに出題されます。
- 画びょう
力が加わる面積を小さくした道具。弱い力で壁に穴をあけることができます。 - スキー
力が加わる面積を大きくした道具。力を分散させることで、雪に足がめり込むのを防ぎます。



コメント