【定期テスト対策問題】平行四辺形の性質を使った証明問題

【定期テスト対策問題】平行四辺形の性質を使った証明・平行四辺形になることの証明です。

【対策問題】平行四辺形の証明
1. 【解答・解説】平行四辺形の証明

【対策問題】平行四辺形の証明

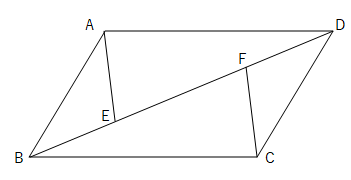
【1】次の図の平行四辺形ＡＢＣＤの対策線ＢＤ上に、点Ｅ、ＦをＢＥ＝ＤＦとなるようにとります。このとき、ＡＥ＝ＣＦであることを証明せよ。

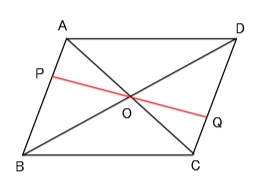
【2】平行四辺形ABCDで, 対角線の交点Oを通る直線を,右の図のようにひき, ２辺AB, CD との交点を, それぞれ, P, Q とします。このとき, OP＝OQ となることを証明しなさい。

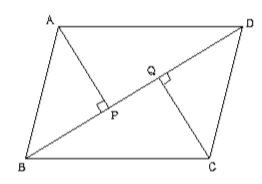
【3】図のように, 平行四辺形ABCDの頂点A, Cから対角線BDに, それぞれ垂線AP, CQをひくとき, AP＝CQであることを次のように証明しました。(　　　）にあてはまるものを書きなさい。

△ABP と（ア）で,
平行四辺形の性質から( イ）………①
平行線の ( ウ）は等しいから( エ）………②
仮定から, ( オ）＝90°………③
①,②,③ から, 直角三角形の ( カ）が,
それぞれ等しいので, △ABP≡( ア）よって, ( キ）

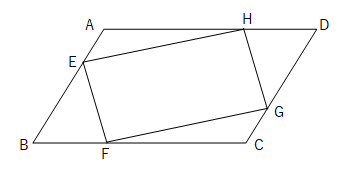
【4】平行四辺形ABCDの辺AB, CD, DA 上に, それぞれ,点E, F, G, H を,AE＝CG, BF＝DHとなるようにとります。このとき, 四角形EFGHは, どんな四角形になりますか。証明し答えなさい。

【5】次のような四角形ＡＢＣＤは、平行四辺形であるといえるか答えよ。

ＡＢ＝5ｃｍ、ＣＤ＝5ｃｍ、ＡＤ//ＢＣ
ＡＢ＝5ｃｍ、ＣＤ＝5ｃｍ、∠Ｂ＝60°、∠Ｃ＝120°
∠Ａ＝∠Ｃ＝70°、∠Ｂ＝110°
∠Ａ＝∠Ｂ＝70°、∠Ｃ＝110°

【解答・解説】平行四辺形の証明

【1】
△ＡＢＥと△ＣＤＦで、
仮定より、ＢＥ＝ＤＦ…①
ＡＢ//ＤＣより錯角が等しいので、∠ＡＢＥ＝∠ＣＤＦ…②
平行四辺形の向かい合う辺は等しいので、ＡＢ＝ＣＤ…③
①②③より２組の辺とその間の角がそれぞれ等しいので
△ＡＢＥ≡△ＣＤＦ
合同な図形では、対応する辺は等しいので、ＡＥ＝ＣＦ

【2】
△AOP と △COQ で,
平行四辺形の対角線は, それぞれの中点で交わるから, AO＝CO ……………… ①
AB // CD だから∠AOP＝∠COQ ……… ②
対頂角は等しいから,∠AOP＝∠COQ ……… ③
①, ②, ③ より, １辺と両端の角がそれぞれ等しいから
△AOP≡△COQ
よって, OP＝OQ

【3】
ア △CDQ
イ AB＝CD
ウ錯角
エ　∠ABP＝∠CDQ
オ　∠APB＝∠CQD
カ　斜辺と1つの鋭角
キ　AP＝CQ

【4】
△AEHと△CGFにおいて
仮定より、AE＝CG…①
平行四辺形の向かいあう角は等しいから、∠ＥAＨ＝∠ＧCＦ…②
また,AD＝BC,かつHD＝BF だからAH＝CF…③
① ② ③ より、２辺とその間の角がそれぞれ等しいから
△AEH≡△CGF
EH＝FG…④
同様にして,△BEF≡△DGHよって, EF＝HG…⑤
④,⑤より,２組の向かいあう辺がそれぞれ等しいから、
四角形EFGHは平行四辺形である。

【5】