【中2数学】平行四辺形の証明のポイントと練習問題

平行四辺形の定義・性質（定理）・条件の比較と違いです。定期テストでは、テスト範囲になっていれば、必ずと言って出題されるわけですが、しっかりその違いを把握していないとなかなか満点といかないようです。確実におさえておく必要があります。それでは、平行四辺形の定義・性質（定理）・条件の比較と違いです。

平行四辺形のポイント
【練習問題】平行四辺形の証明
1. 【解答・解説】平行四辺形の証明
2. 平行四辺形のなかま

平行四辺形のポイント

図形	定義	性質（定理）	条件
平行四辺形	2組の対辺（向かい合う辺）がそれぞれ平行な四角形	２組の対辺（向かい合う辺）はそれぞれ等しい。	2組の対辺（向かい合う辺）がそれぞれ平行
		２組の対角（向かい合う角）はそれぞれ等しい。	２組の対辺（向かい合う辺）はそれぞれ等しい。
		対角線はそれぞれ（おのおの）の中点で交わる。	２組の対角（向かい合う角）はそれぞれ等しい。
			対角線はそれぞれ（おのおの）の中点で交わる。
			１組の対辺（向かい合う辺）が平行でその長さが等しい。

平行四辺形の証明では、平行線の性質のうち、錯覚や同位角がそれぞれ等しいということや対頂角は等しいということは知っておく必要があります。平行四辺形の証明では、ほぼ100％使うと思っていていいでしょう。

次の平行四辺形に関する証明は、「平行四辺形の性質をつかっておこなう証明」と「平行四辺形になることを証明」と大きく2つあります。

【練習問題】平行四辺形の証明

1.平行四辺形の性質を使って行う証明
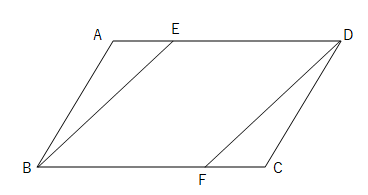
次の図の平行四辺形ＡＢＣＤの辺ＡＤ，ＢＣ上にＡＥ＝ＣＦとなるように点Ｅ、Ｆをとるとき、ＢＥ＝ＤＦになることを証明せよ。

2.平行四辺形であることの証明
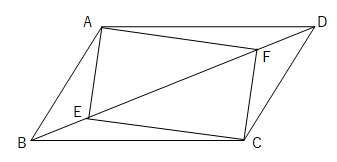
平行四辺形ＡＢＣＤの対角線ＢＤ上に点Ｅ、ＦをＢＥ＝ＤＦとなるようにとります。このとき、四角形ＡＥＣＦは平行四辺形であることを証明しなさい。

【解答・解説】平行四辺形の証明

1.平行四辺形の性質を使って行う証明
△ＡＢＥと△ＣＤＦで、
仮定より、ＡＥ＝ＣＦ…①
平行四辺形の向かい合う辺は等しいので、ＡＢ＝ＣＤ…②
平行四辺形の向かい合う角は等しいので、∠ＥＡＢ＝∠ＦＣＤ…③
①②③より２組の辺とその間の角がそれぞれ等しいので
△ＡＢＥ≡△ＣＤＦ
合同な図形では、対応する辺は等しいので、ＢＥ＝ＤＦ

2.平行四辺形であることの証明
点ＡとＣを結び、ＢＤとの交点をＯとする。
四角形ＡＢＣＤは平行四辺形だから
ＡＯ＝ＣＯ…①
ＢＯ＝ＤＯ…②
ＥＯ＝ＢＯ－ＢＥ、ＦＯ＝ＤＯ－ＤＦより、ＢＥ＝ＤＦ…③
②③より、ＥＯ＝ＦＯ…④
①④より、対角線が、それぞれの中点で交わるので、四角形ＡＥＣＦは平行四辺形です。