地震に関する問題です。まずは基礎知識の確認を行い、実戦型の地震の問題に挑戦しましょう。計算に力を入れた問題も準備しています。
ポイント 【中1理科】地震波の速さ・地震発生時刻・初期微動継続時間の求め方
【対策問題】地震の計算問題
[問題]下のグラフは、ある地震の2つの波が伝わる速さを記録したものである。これについて、次の各問いに答えなさい。
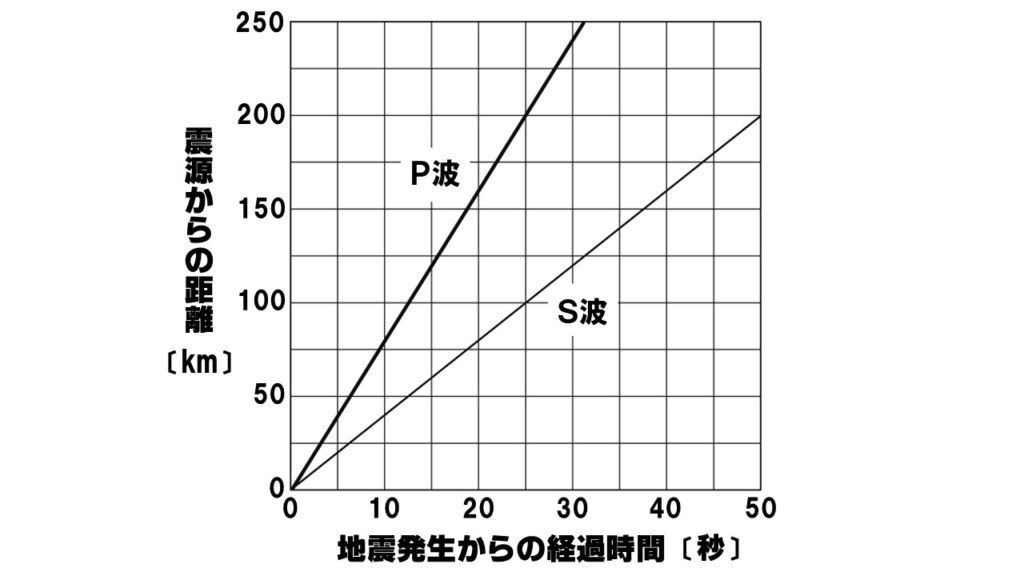
(1)観測地点にP波、S波が到着すると、それぞれ何というゆれが始まるか。
(2)この地震のP波とS波の伝わる速さをそれぞれ求めよ。
(3)P波が到着してからS波が到着するまでの時間を何というか。
(4)(3)の時間と震源からの距離にはどんな関係があるか。
(5)(3)の時間が25秒になるのは、震源からの距離が何kmの地点か。
(6)震源からの距離が320km地点での(3)の時間は何秒になるか。
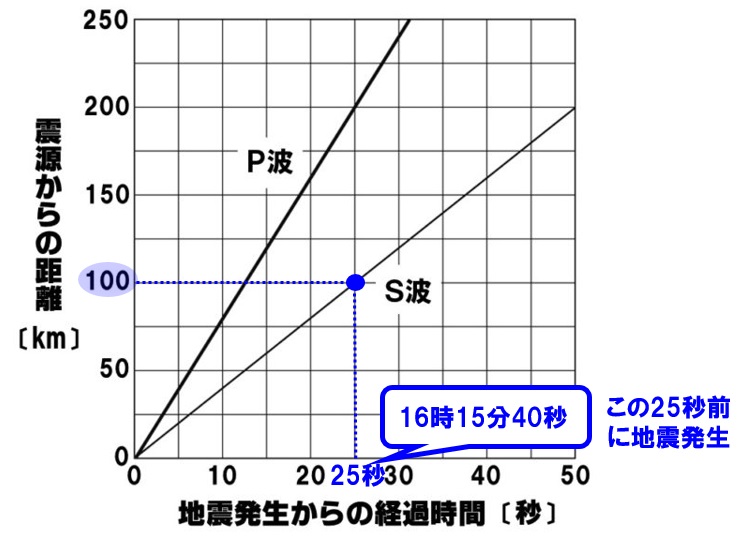
(7)震源から100km離れた地点にS波が到着した時刻は16時15分40秒であった。この地震の発生時刻は何時何分何秒か。
(8)観測地点でのゆれの程度を何というか。
(9)この地震の規模を表すマグニチュードはM6であった。M6の地震はM4の地震のエネルギーの約何倍か。次の中から一つ選べ。
ア 4倍 イ 32倍 ウ 64倍 エ 1000倍 オ 32000倍
(10)この地震とは別の地震が発生した。初期微動が続く時間が前回の地震よりも短くなったが、震度は前の地震と同じであった。今回発生した地震の震源からの距離とマグニチュードについてわかることを簡潔に答えよ。
【解答・解説】地震の計算問題
(1)P波:初期微動 S波:主要動
速い波であるP波が伝わると地震の最初のゆれ初期微動が起こります。遅い波であるS波が伝わると大きな揺れ主要動が起こります。
・遅い波:S波→大きなゆれ:主要動
(2)P波:8km/s S波:4km/s
グラフより、P波は200kmの道のりを25秒で進んでいるので、
200km÷25秒=8km/s
グラフより、S波は100kmの道のりを25秒で進んでいるので、
100km÷25秒=4km/s
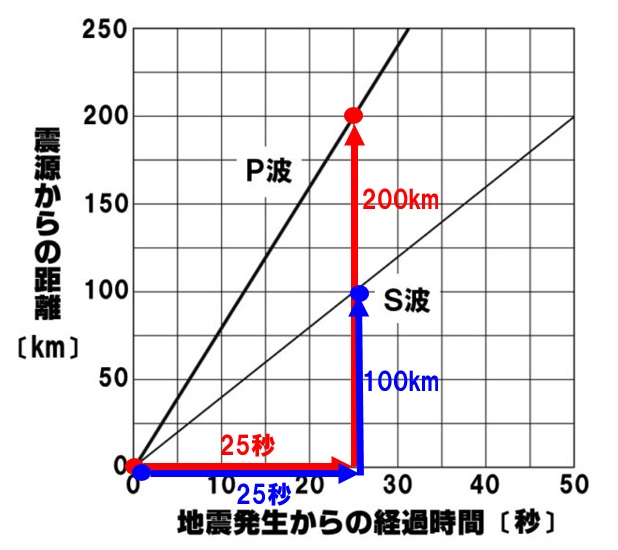
(3)初期微動継続時間
初期微動が到着してから主要動が到着するまでの時間を初期微動継続時間といい、P波による小さな揺れ初期微動が続く時間になります。
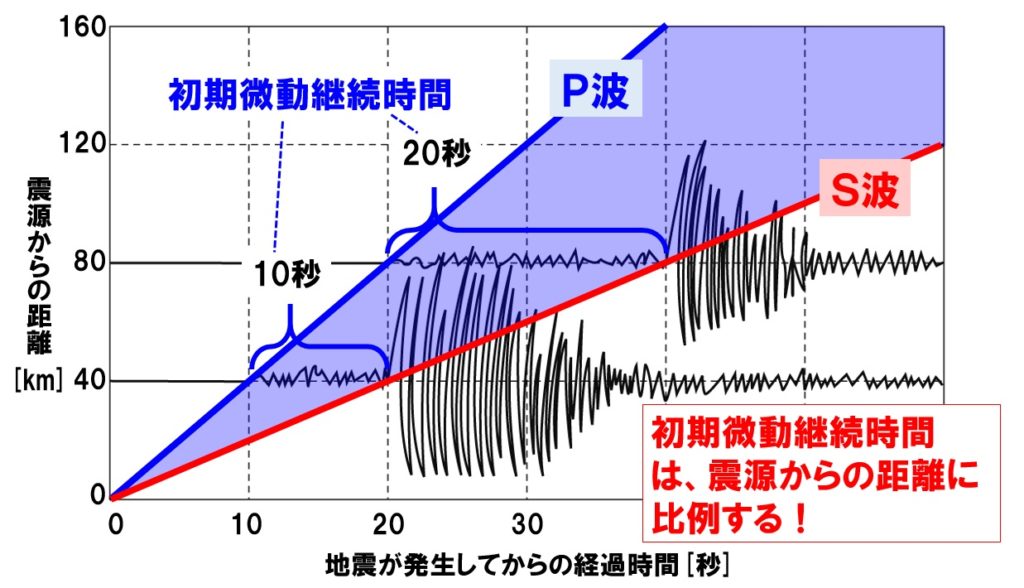
(4)初期微動継続時間と震源からの距離は比例する。
震源からの距離が2倍、3倍になると、初期微動継続時間も2倍、3倍になります。
(5)200km
グラフより、P波が到着してからS波が到着するまでの時間差が25秒になっているのは200km地点になっています。
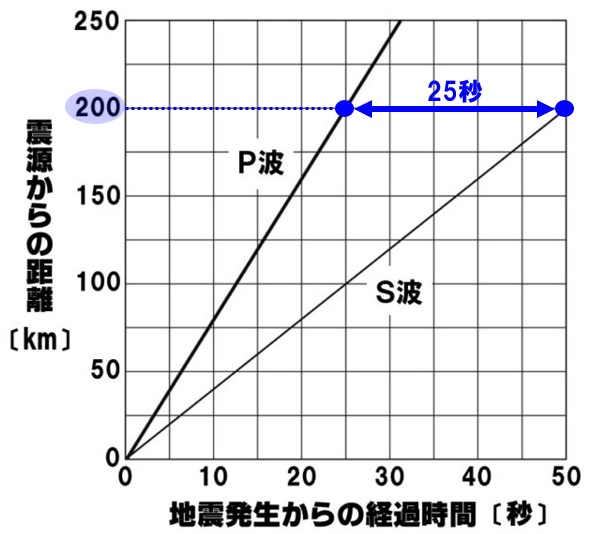
(6)40秒
震源からの距離と初期微動継続時間は比例するので、
200km:25秒=320km:x秒
これを解くとx=40秒
(7)16時15分15秒
グラフより、100km地点にS波が到着したのは地震が発生してから25秒後だとわかる。つまり100km地点にS波が到着した時刻の25秒前に地震が発生したとわかる。
16時15分40秒ー25秒=16時15分15秒
(8)震度
観測地点でのゆれの程度を震度といいます。震度は日本では、震度0~震度7(震度5と震度6は強弱に分かれる)の10段階で表示されます。
・マグニチュード…地震の規模(エネルギーの大きさ)
(9)エ
マグニチュードが1大きくなると、そのエネルギーは約32倍になる。マグニチュードが2大きくなると、そのエネルギーは約32倍の約32倍、約1000倍大きくなります。
・エネルギーが2大きくなると→エネルギーは約32倍×32倍=約1000倍
・エネルギーが3大きくなると→エネルギーは約32倍×32倍×32倍=約32000倍
(10)震源からの距離は近くなり、マグニチュードは小さかった。
初期微動継続時間が短いことから、震源までの距離は近いことがわかります。また。近い場所で起こった地震にもかかわらず震度が同じだったことより、前に起こった地震よりもマグニチュードが小さいことがわかります。


コメント