【中1理科】凸レンズの仕組みを徹底解説！実像・虚像の特徴＆テスト対策問題付き

今回は、光の性質で登場する凸レンズ、凸レンズでできる像「実像」「虚像」について学習します。光の屈折を利用した作図ができるようになると、実像や虚像の問題もすんなりと解けるようになります。

凸レンズ

凸レンズとは、中心が膨らんだレンズで、光の屈折を利用した道具になります。虫眼鏡や顕微鏡などに利用されています。まずは下の図で用語を覚えましょう。

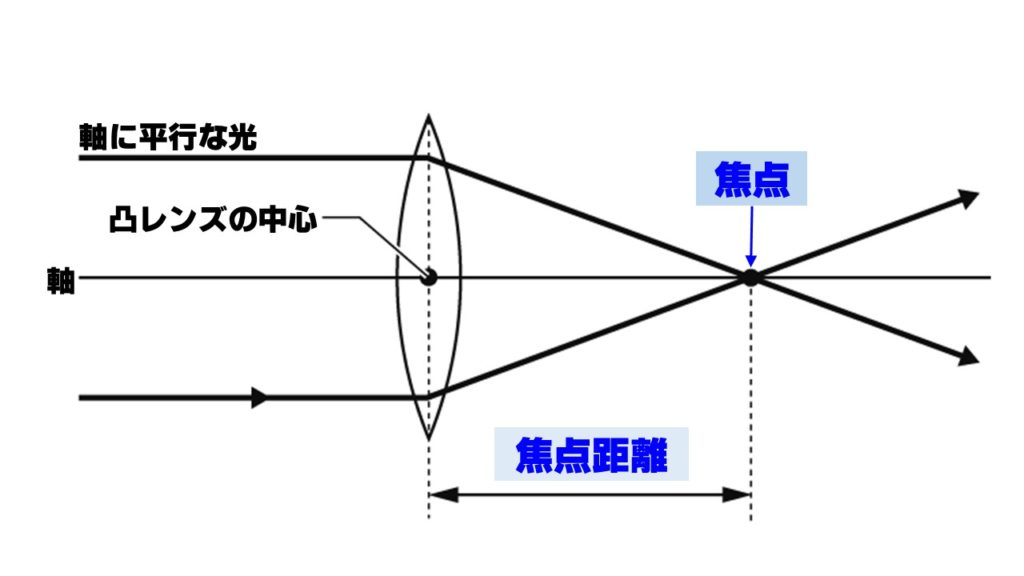
• 焦点
  軸に平行な光が集まる点。小さいころ虫眼鏡で太陽の光を集めて、黒い紙を燃やした経験はありませんか？あの光が集まる点が焦点になります。焦点は凸レンズの左右に1つずつ存在します。
• 焦点距離
  凸レンズの中心から、焦点までの距離を焦点距離といいます。凸レンズが厚いほど、焦点距離が短くなり、凸レンズが薄いほど焦点距離は長くなります。

凸レンズでの光の屈折

凸レンズは光の屈折を利用したものです。凸レンズを通過した光がどのように進むのか、基本の作図をマスターしましょう。

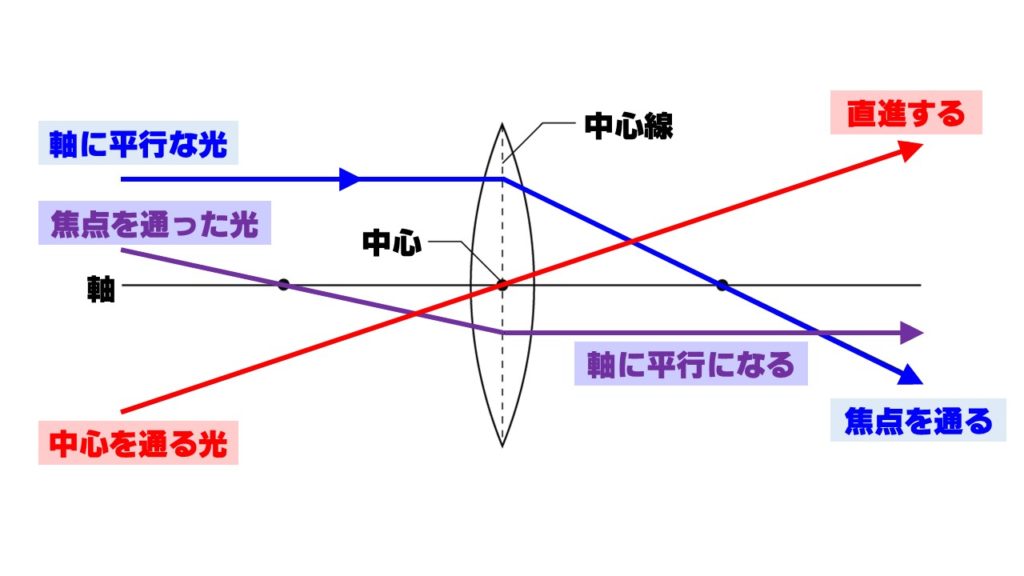
1. レンズの中心を通過する光→直進する
2. 軸に平行な光→レンズの中心線で屈折し焦点を通る
3. 焦点を通過してきた光→軸に平行に進む

この3つの作図ができれば、この後の実像の作図や、虚像の作図もできるようになります。まずはこの3つをしっかりマスターしてください。

実像の作図

実像とは、凸レンズを通過した光が屈折し、光が集まってできる上下左右が逆の像です。

実際に光が集まってできる像ですので、スクリーンやついたてなどに映すことができる像になります。次の手順で作図します。

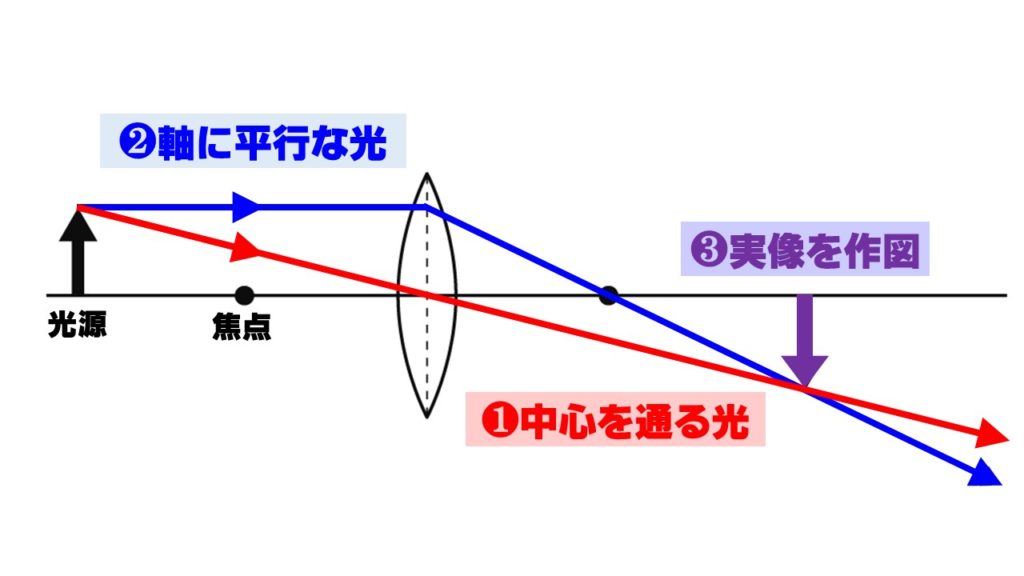
焦点を作図させる問題にも対応できるように、必ずこの手順で作図する習慣をつけておきましょう。

虚像の作図

虚像とは、凸レンズ越しに見える、光源と上下左右が同じ向きのそこにあるかのように見える像です。

実際に光がそこから出ているのではないのでスクリーンに映すことはできません。虫眼鏡で拡大されて見える像は虚像になります。虚像は次の手順で作図します。

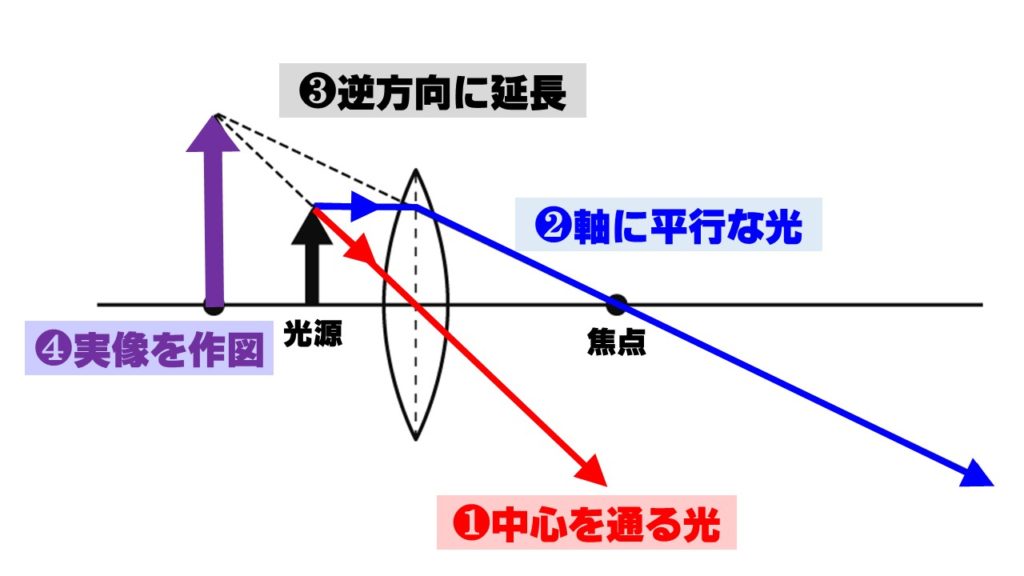
まずはここまでの作図をしっかりとマスターしましょう。そうすれば、下記の「凸レンズに関する問題」もスムーズに解けるようになってきます。

ちなみに、焦点上に光源を置いた場合、❶と❷の光が平行になるので、実像も虚像もできないことも覚えておきましょう。

実像と虚像

光の屈折を利用した道具「凸レンズ」では、2つの像が観察できます。

• 実像（じつぞう）
• 虚像（きょぞう）

実像は、実際に凸レンズを通過して集まった光がつくる像で、スクリーンに映すことができる像です。凸レンズで光学屈折しひっくり返って像ができるので、「倒立実像」ともいったりします。

虚像は、凸レンズ越しに見える、そこにあるかのように見える像です。実際にそこから光が出ているわけではないので、スクリーンに映すことはできません。実際の光源よりも大きく見え、向きも光源と同じ向きに見えるので、「正立虚像」ともいわれます。

実像の大きさと光源の位置との関係

光源と凸レンズの距離関係で、実像の大きさがどのように変化するのかを考えるとき、基本となるのが「焦点距離の2倍の位置」です。ここに光源を置いた場合、凸レンズと光源の距離と、凸レンズと実像との距離の大きさが等しくなります。また、できる実像の大きさも光源と同じになります。

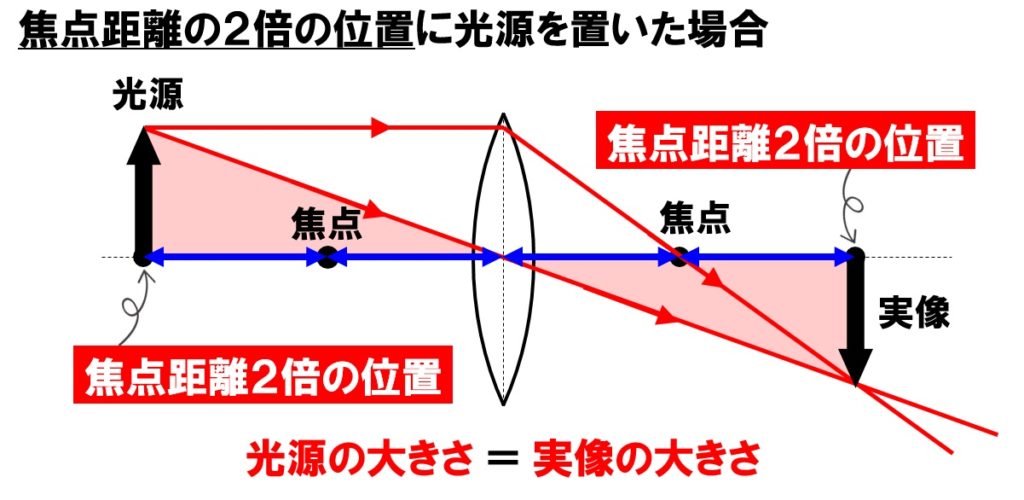
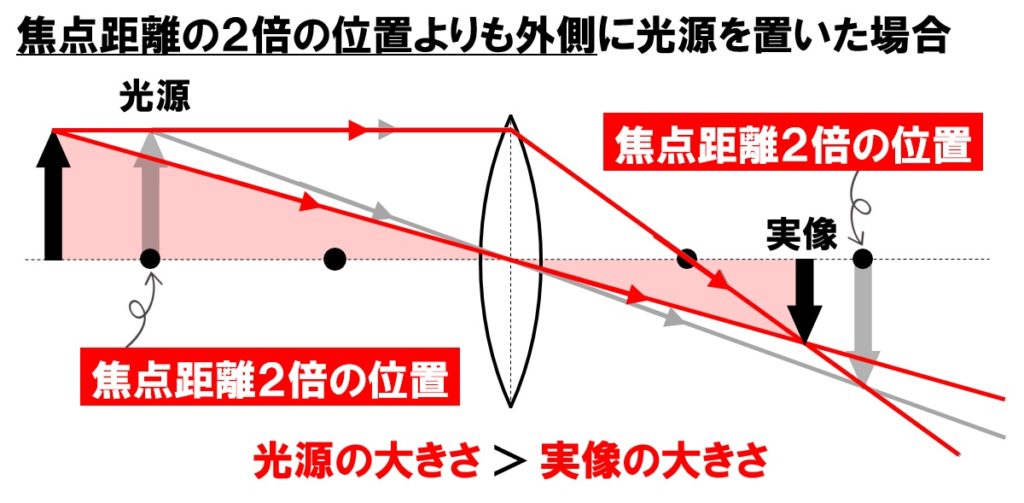
焦点距離の2倍の位置よりも、光源を外側に置いた場合には、焦点距離の2倍の位置よりも内側に（凸レンズに近い位置）に実像ができます。このときできる実像の大きさは、光源の大きさよりも小さくなります。下の図を参考にしてください。

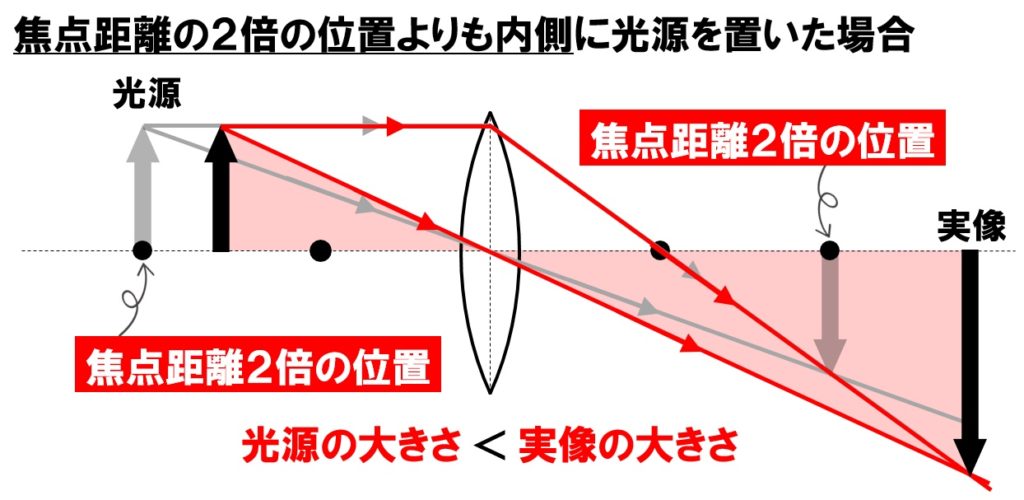
次は、焦点距離の2倍の位置よりも内側に光源を置いた場合です。このとき実像は、焦点距離の2倍の位置よりも外側に実像ができます。できる実像の大きさは、実際の光源の大きさよりも大きくなります。

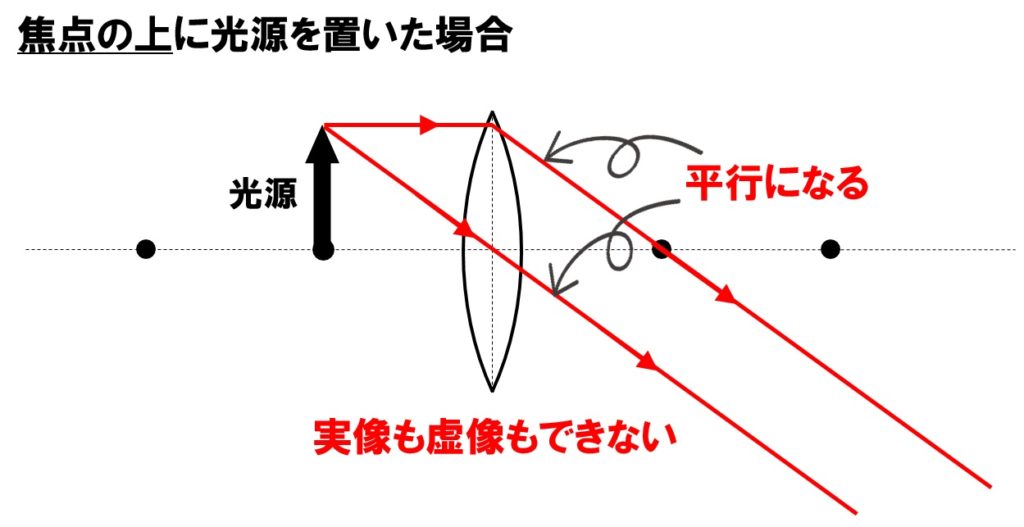
焦点上に光源を置いた場合はどうなるのでしょうか。焦点上に光源を置いた場合は、凸レンズの中心を通る光も、軸に平行に進み凸レンズで屈折し焦点を通った光も、平行になります。光が集まらないので実像はできなくなります。また、光が進んできた方向と逆方向に延長しても平行な光なので、虚像もできません。

虚像の大きさと光源の位置との関係

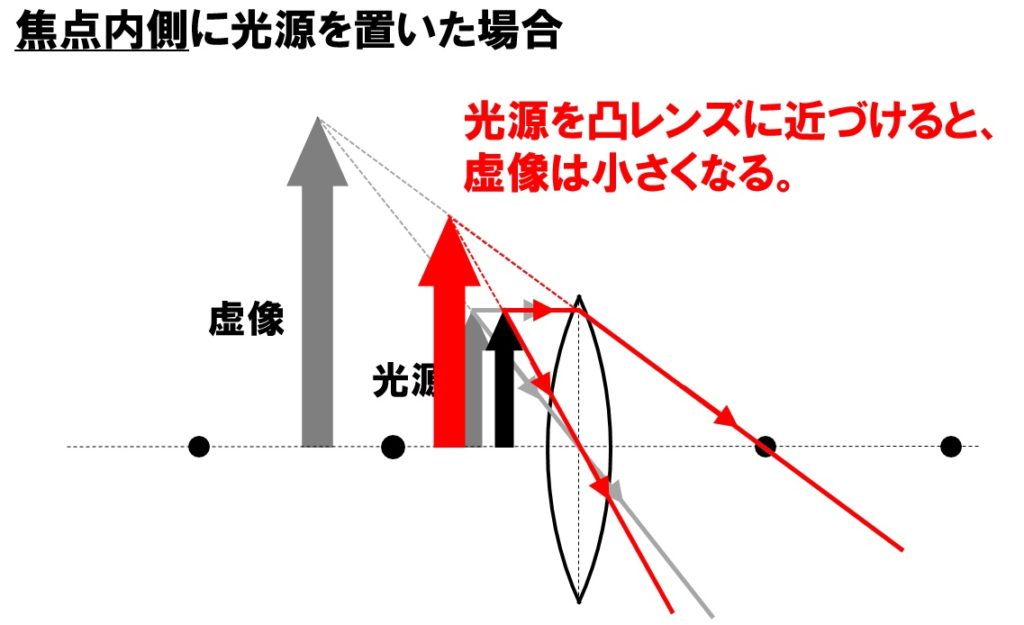
最後に、虚像の大きさについて考えます。焦点距離よりも内側（凸レンズに近い位置）に光源を置いた場合は虚像ができますが、光源をさらに凸レンズに近づけた場合、虚像の大きさはどうなるのでしょうか。下の作図を見れば、光源を凸レンズに近づければ近づけるほど、できる虚像の大きさは小さくなります。遠ざければ、虚像の大きさは大きくなります。

以上が凸レンズのポイントになります。

ここから先は発展内容になります。普通の教科書では登場しませんので、必要な人のみ勉強しましょう。

［発展内容］望遠鏡

遠くの物体を拡大してみることができる望遠鏡は、凸レンズや凹レンズ、反射鏡などを組み合わせてできています。凸レンズや凹レンズなどレンズだけを使った望遠鏡を屈折望遠鏡、反射鏡とレンズの両方を用いたものを反射望遠鏡といいます。

屈折望遠鏡には、対物レンズと接眼レンズともに凸レンズのケプラー式望遠鏡と、対物レンズは凸レンズ、接眼レンズが凹レンズのガリレイ式望遠鏡があります。天体望遠鏡などの遠くの物体を観察する場合は、像が上下左右逆（倒立）に見えるケプラー式、地上の物体を観察する場合は、像がそのままの向き（正立）に見えるガリレイ式が用いられます。

望遠鏡のしくみ

次のしくみにより、遠くにある物体を大きく拡大して観察することができます。

1. 対物レンズによって遠くの物体の実像をつくる。
2. その実像を接眼レンズの焦点距離の内側で観察することで、拡大された虚像が見える。

望遠鏡だけではく、微生物を観察するときに使用する顕微鏡なども同じ仕組みでできています。詳しくは次のケプラー式望遠鏡のしくみで学習します

ケプラー式望遠鏡のしくみ

ケプラー式望遠鏡は、対物レンズと接眼レンズがともに凸レンズの望遠鏡で、しくみが簡単なので高校入試などでも出題されることがあります。

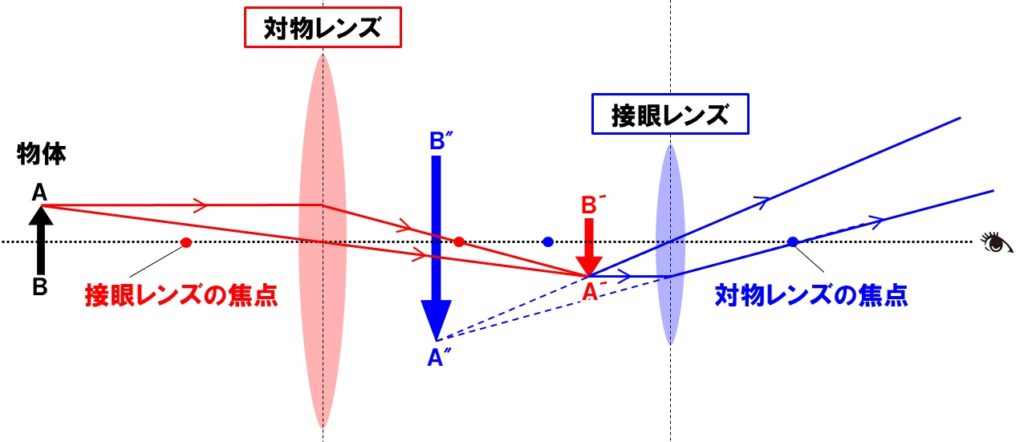
1. 対物レンズによって、遠くにある物体ABの実像A´B´が接眼レンズの焦点距離内にできる。
2. 接眼レンズを通して実像A´B´を観察すると大きな虚像A”B”が見える。

実像と虚像を上手く利用して遠くの物体を拡大してみているわけです。顕微鏡のつくりもこの仕組みと同じになります。

【対策問題】凸レンズの応用

下の図のように、光源とスクリーンの間に凸レンズを置き、光源と凸レンズの距離ａをいろいろ変えて、像がはっきりとできる位置にスクリーンを移動させた。このときの凸レンズとスクリーン間の距離をｂとし、像の高さを測定した。表はその結果をまとめたものである。これについて、後の各問いに答えよ。

ａ［cm］	16	18	20	24	28	36
ｂ［cm］	48	36	30	24	C	18
像の高さ［cm］	12	8	B	4	3	2

（1）この実験のように、スクリーンに映る逆さの像のことを何というか。

（2）この凸レンズの焦点距離は何cmか。

（3）この光源の高さは何cmか。

（4）表のBのときの倍率は何倍か。

（5）表のBの値を求めよ。

（6）表のCの値を求めよ。

【解答・解説❷】凸レンズの応用

（1）実像

光源から出た光はあらゆる方向に拡散していきますが、凸レンズを通過した光は屈折し、1つの点に集まります。ここにできるのが実像で、上下左右が逆向きで、スクリーンに実際に映すことができる像になります。

（2）12cm

焦点距離の2倍の位置に光源を置いた場合、凸レンズから光源までの距離（ａ）と凸レンズから実像までの距離（ｂ）が等しくなります。表を確認すると、ａとｂの距離が等しくなっているのは24cmのときです。したがって、焦点距離はその半分の距離12cmとなります。

（3）4cm

焦点距離の2倍の位置に光源を置いた場合、凸レンズから光源までの距離（ａ）と凸レンズから実像までの距離（ｂ）が等しくなり、できる実像の大きさは光源と同じ大きさになります。したがって、ａとｂが24cmのときの像の大きさが4cmなので、光源の大きさも4cmになります。

（4）1.5倍

凸レンズの倍率は、実像の大きさ（B）/光源の大きさ（A）、または、凸レンズと実像までの距離（ｂ）/凸レンズと光源までの距離（ａ）で求めることができます。表で像の高さがＢのとき、凸レンズと実像までの距離（ｂ）/凸レンズと光源までの距離（ａ）＝30/20となり1.5倍になります。また、作図をして相似を使って求めることもできます。

（5）6cm

倍率が（4）で1.5倍と分かったので、光源の大きさ4cmを1.5倍し、6cmになるとわかります。上の図のように相似を使って求めてもいいでしょう。

（6）21cm

凸レンズの公式、1/ａ＋1/ｂ＝1/ｆ　代入すると、
1/28＋1/Ｃ＝1/12
1/Ｃ＝7/84＋3/84
1/Ｃ＝4/84＝1/21
Ｃ＝21
となります。
また、下の図のように作図を行い、相似を使って解いていってもいいでしょう。