今日は力の単元で登場する「ばね」について学習を進めていきます。ばねといえば、有名な「フックの法則」が登場します。
ばねにはたらく力
ばねに力を入れて引っ張たり、押し縮めたりすると元に戻ろうとする力がはたらきます。この物体が元に戻ろうとする性質を弾性、その力を弾性力といいます。
ばねにはたらく弾性力は、ばねが伸びれば伸びるほど、縮まれば縮まるほど大きくなります。つまり、これはフックの法則と呼ばれています。
フックの法則
フックの法則とは、ばねののびと弾性力の大きさが比例するということです。気をつけたいのが、「ばねの長さ」ではなく「ばねののび」と比例することです。このフックの法則を式にすると比例の式になります。
弾性力=kx
※k…ばね定数(ばねの硬さを表す)
※x…ばねののび・ちぢみ
❷ばねののびと弾性力の大きさは比例する(フックの法則)
問題によって、ばねののびを聞いてくる問題とばねの長さを聞いてくる問題がありますので注意が必要です。
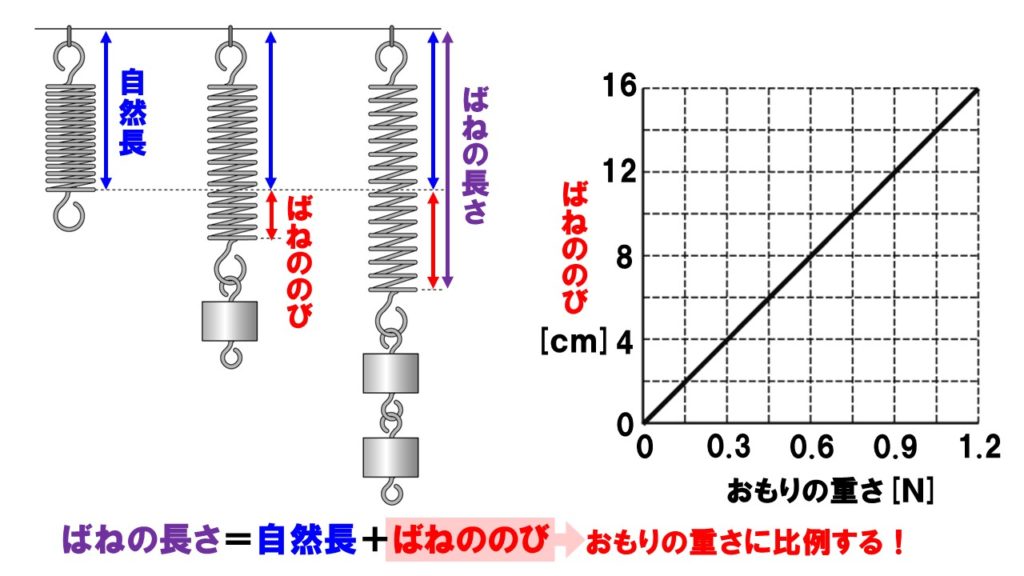
自然長
ばねに何もつるしていないときの、ばね自体の長さのことを自然長といいます。ばねの長さを求める問題では、ばねののびに自然長を足すことで、ばねの長さを求めることができます。また、ばねの長さが与えられた場合、フックの法則を使って計算するためには、自然長を引いてばねののびに直す必要があります。
自然長=ばねの長さ-ばねののび
ばねののび
自然長の状態から伸びて長くなった部分がばねののびになります。ばねののびとおもりの重さにはフックの法則が成り立ちます。つまり、ばねののびとおもりの重さには比例関係があります。ばねの長さが与えられた場合、自然長を引いてばねの長さにします。
ばねののび=ばねの長さ-自然長
ばねの長さ
おもりをつるしたときのばね全体の長さです。もともとの自然長も、おもりをつるしたことによるのびも、すべて足し合わせた長さになります。ばねの長さを求める場合、フックの法則で計算したばねののびに、自然長を足す必要があります。
ばねの長さ=ばねののび+自然長
ばねの直列つなぎ・並列つなぎ
ばねののび、フックの法則の問題では、ばねを2本使った応用問題が出題されます。まっすぐ縦に2本つないだ「直列つなぎ」と、横に並べて2本つないだ「並列つなぎ」になります。
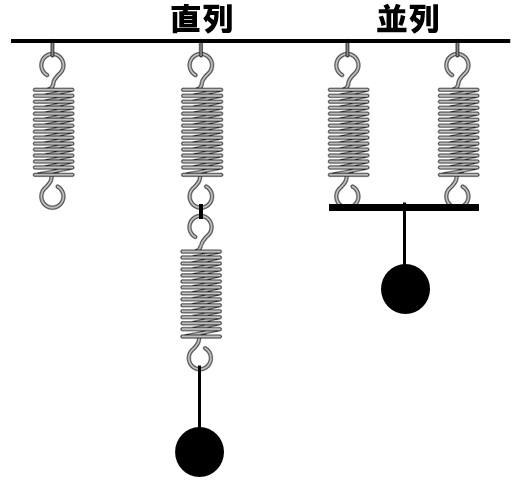
ばねを直列につないだ場合と、並列につないだ場合では、ばねがどのようにのびるのか簡単にみていきましょう。ばね自体の重さは無視できるものとして考えていきましょう。
ばねの直列つなぎ
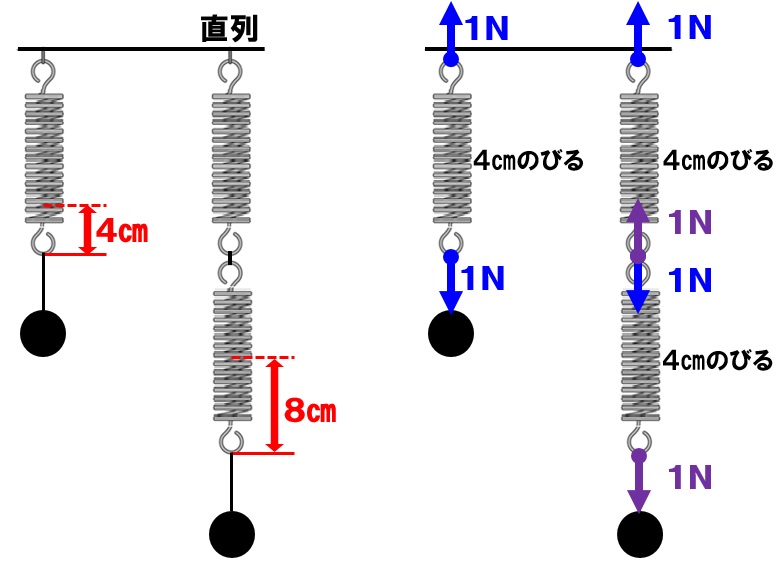
同じばねを直列につないだ場合、2本のばねの伸びの合計は、1本のときの2倍になります。例えば、1Nのおもりをつり下げると4cm伸びるばねがあったとします。このばねを2本直列につなぎ1Nのおもりをつり下げると、2本のばねの伸びの合計は8cmになります。
これは、直列にばねをつないだ場合、2本のばねそれぞれに1Nの力が加わるからです。なので、それぞれ4cmずつ伸び、合計で2倍の8cm伸びるわけです。
ばねの並列つなぎ
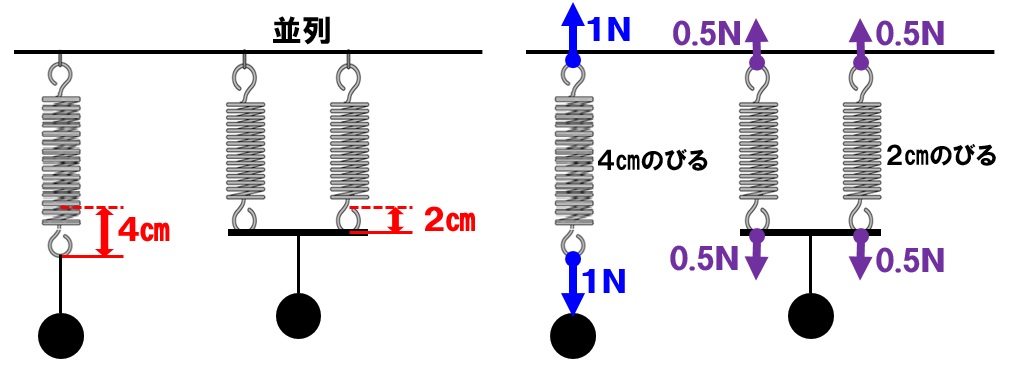
同じばねを並列につないだ場合、2本のばねの伸びは、それぞれ1本のときの1/2倍になります。例えば、1Nのおもりをつり下げると4cm伸びるばねがあったとします。このばねを2本並列につなぎ1Nのおもりをつり下げると、2本のばねはそれぞれ2cmずつのびることになります。
これは、並列にばねをつないだ場合、2本のばねそれぞれに1Nの半分の0.5Nの力が加わるからです。なので、それぞれ2cmずつ伸びるわけです。
ばねの直列・並列 まとめ
ばねの直列と並列についてまとめると、ばねにある重さのおもりをつり下げるとacmのびたとすると、直列つなぎと並列つなぎに次のようなのびになります。
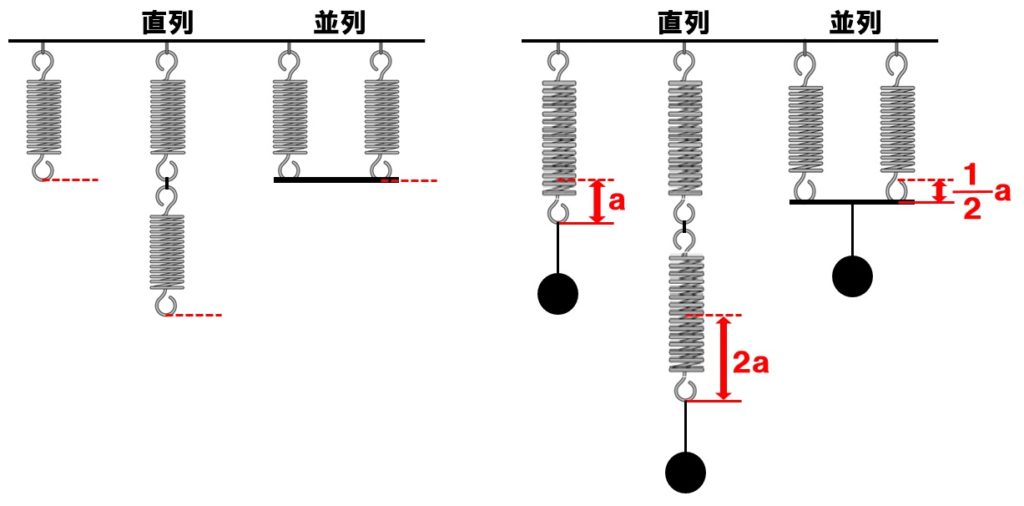
ただし、これは同じばねを使った場合です。伸び方が異なるばねを使った場合は当てはまらないのでそれぞれ計算することになります。
フックの法則を理解するためには演習が必要です。ここまでの知識が実際の問題でどのように使われているの確認しましょう。


コメント