今日のテーマは浮力です。浮力とは、水の中で受ける上向きの力で、計算問題もよく出題されます。4つの計算方法があるので、どんな問題でも計算できるように練習しましょう。
浮力とは
お風呂や海などに入ると、体が水によって押し上げられ軽くなりますよね。このように水中で物体を押し上げようとする力のことを浮力と言います。大きな鉄のかたまりである船が浮かぶのは浮力がはたらいているからです。
浮力が生じるしくみ
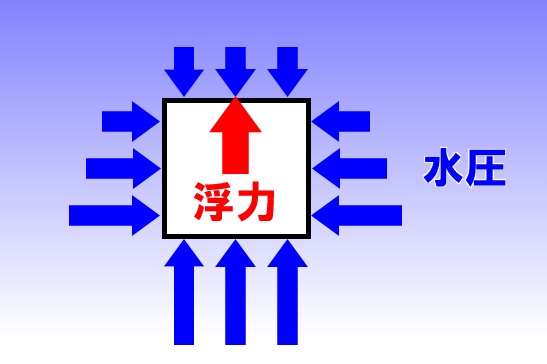
なぜ浮力が生じるかというと、液体の中にある物体には水圧が生じますが、物体の上面にはたらく水圧よりも、物体の下面にはたらく水圧の方が大きく、その差が浮力になるのです。
浮力の計算方法
水の中で受ける上向きの力である浮力の求め方には、4つのパターンがあります。特に最初の2つのパターンは入試でもよく出題される計算です。
- 空気中と水中のばねはかりの差
- 水面に浮かんでいる物体にはたらく浮力
- 上面と下面にはたらく水圧の差
- 押しのけた水の重さ(アルキメデスの原理)
残りの2つのパターンは応用的な計算になりますので、自分の学習の進み具合で、マスターするか飛ばしておくか決めてください。
空気中と水中のばねはかりの差
パターン1として、空気中ではかった物体の重さと、水中ではかったばねはかりの目盛りの差で浮力を計算する問題です。
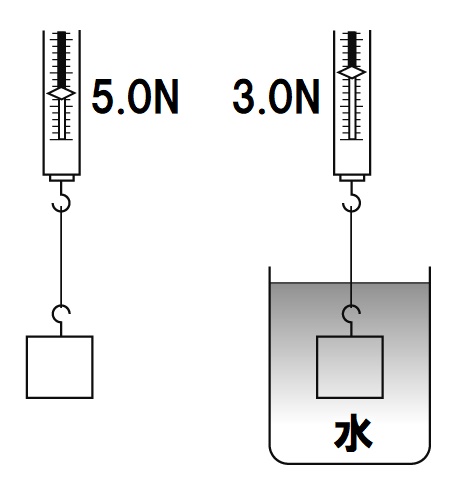
上の図のように、空気中で物体の重さをはかると5.0Nで、物体を水の中に入れると、ばねはかりが3.0Nを示した場合の浮力は次のように計算します
5.0Nー3.0N=2.0N
水面に浮かんでいる物体にはたらく浮力
パターン2です。水面や水中に物体が浮かんで静止している問題です。この計算方法も非常に簡単です。浮かんで静止しているということは、物体にはたらいている重力と、浮力がつり合っています。
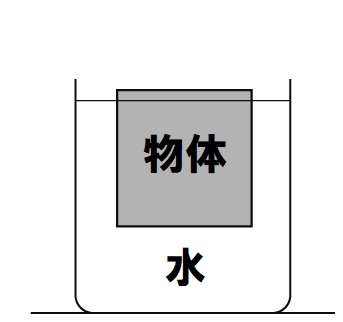
上の図のように、100Nの物体が水面に浮かんで静止している場合の浮力の大きさは、物体の重力と同じ100Nとなります。
物体にはたらく重力100N=物体にはたらく浮力100N
上面と下面にはたらく水圧の差
水の密度や、水面からの深さ、物体の底面積などがわかっている場合は、物体の上面と下面にはたらく水圧の差から浮力を求めることができます。
物体の上面より、下面の方が深い位置にありますので、その分、下面にはたらく水圧の方が大きくなります。この水圧の差分が浮力になるのです。
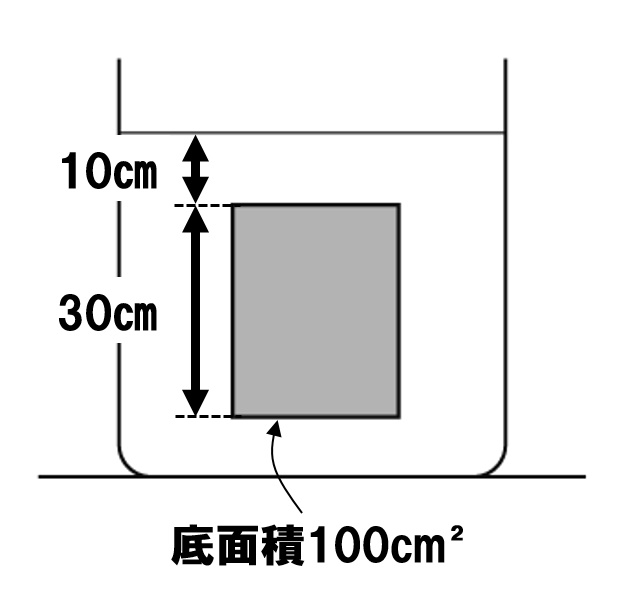
上の図のように、物体が水中にある場合の浮力を計算してみましょう。水の密度を1.0g/cm³、100gの物体にはたらく重力の大きさを1.0Nとします。
物体の上面は、水面から10cmの深さにあるので、
- 100cm²×10cm=1000cm³
- 1000cm³×1.0g/cm³=1000g
- 1000g=10N
上面は、水の重さによって10Nで下向きに押されています。
物体の下面は、水面から10cm+30cm=40cmの深さにあるので、
- 100cm²×40cm=4000cm³
- 4000cm³×1.0g/cm³=4000g
- 4000g=40N
下面は、水の重さによって40Nで上向きに押されます。
したがって、浮力の大きさは、
- 40N-10N=30N
となります。
押しのけた水の重さ(アルキメデスの原理)
水の中につかっている物体の体積がわかる場合は、アルキメデスの原理を使って浮力を計算することができます。
アルキメデスの原理とは、押しのけた液体の重さが浮力になるという法則です。

上の図のように、底面積100cm³、高さが30cmの物体が水中にすべてつかっている場合、浮力の大きさは、
- 100cm²×30cm=3000cm³
- 3000cm³×1.0g/cm³=3000g
- 3000g=30N
物体によって押しのけられた水の重さは30Nになるので、浮力の大きさも30Nとなります。
以上が浮力の計算の方法です。解き方をもう一度確認し、実戦問題に挑戦しましょう。ばねの計算とあわせて出題されることが多いようです。



コメント