【中2数学】一次関数の応用問題（線分が等しくなる座標を求める）

【中2数学】一次関数の応用問題（線分が等しくなる座標を求める）です。

【問題】線分が等しくなる座標を求める（中2一次関数）

図のように直線ℓであるy=−1/2x+6と直線ｍであるy＝2x-2がある。x軸上の点Pを通り、y軸に平行な直線を引き、ℓ、mとの交点をそれぞれQ、Rとする。点Pのx座標をkとして次の問いに答えなさい。

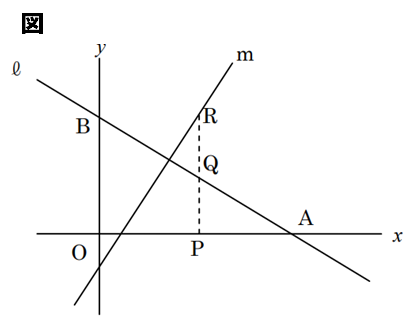
(1)点Q、点Rの座標をkで表しなさい。

(2)RQ＝2になるときkの値を求めなさい。

(3)RQ＝PQとなるときのkの値を求めなさい。

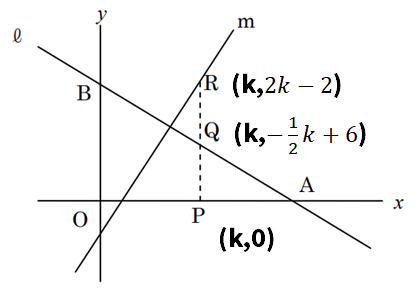
（1）Q:(k,-1/2k+6) R(k,2k-2)
x座標は、kであることが分かっている（座標pのx＝kかつ、y軸に平行な直線）ので、それぞれx=kを代入して求める。（点Qは、y=−1/2x+6に、点Rは、y＝2x-2に）

（2）k=4

(2k-2)-(-1/2k+6)=2の方程式を解く。

（3）k=14/3
(2k-2)-(-1/2k+6)=(-1/2k+6)-0の方程式を解く。